Correção comentada da prova de matemática do ENEM 2016 através do caderno azul:
/i.s3.glbimg.com/v1/AUTH_59edd422c0c84a879bd37670ae4f538a/internal_photos/bs/2016/M/O/dAlo0fQPiGPmjHgGN5HQ/enem2016-136.jpg)
(Clique na imagem para expandir)
136) Aqui temos um problema muito corriqueiro de cálculos envolvendo a geometria espacial.
No caso, o sólido seria um silo de grãos que é formado por um cilindro com um cone pelo topo.
O problema foi tão bondoso que deixou de graça todas as medidas de ambos sólidos: alturas e raio da circunferência!
A questão quer saber quantas viagens um caminhão que suporta apenas 20m³ de carga teria que fazer para carregar todo o grão suportado pelo volume total do silo.
Para saber disso, basta apenas calcularmos o volume do silo que seria o volume de seu cilindro (V1) e de seu cone (V2):
Calculando volume do cilindro:
V1 = AB * h
Como se trata de um cilindro, seu volume em AB é dado por pi r², então:
V1 = 3 * 3² * 12 = 324
Calculando volume do cone que tem como fórmula:
V2 = AB*h/3 ou seja:
V2 = 3*3²*3/3 = 27
O silo é a soma do volume do cone com o volume do cilindro (V1 e V2) então temos que V1 + V2 = 351
Se o caminhão capacita até 20m³ de carga, quantas viagens ele faria para suportar 351m³ de carga?
Basta aplicar uma regra de três para resolver:
20 --- 1 viagem
351 --- x viagens;
20x = 351
x = 351/20 = 17,55
Alerta de pegadinha: Marcando a letra C (17 viagens) você estaria errando, pois o resultado não deu 17 viagens exatas, mas sim 17.55, portanto a resposta certa é a D: 18 viagens!!!!
Resposta: Letra D
/i.s3.glbimg.com/v1/AUTH_59edd422c0c84a879bd37670ae4f538a/internal_photos/bs/2016/b/P/w02EcjRLeoaWE9ll8hiw/enem2016-137.jpg)
(Clique na imagem para expandir)
137) É um problema de escala.
Foram dadas as dimensões do guarda-roupa: 220cm altura, 120cm largura e 50cm de profundidade como dito no problema.
Esse guarda-roupas foi projetado numa escala de 1 para 8 (1:8) e mesmo assim não coube na folha para impressão, e tendo isso como problema, seu projetista ajustou a impressão para diminuir 20% do tamanho do desenho, e então o problema pergunta, depois dessa redução... Quanto passou a ser as dimensões projetadas deste guarda-roupas?
Se temos uma escala de 1:8 em todas as dimensões reais do objeto, então para saber as dimensões projetadas basta dividir todos seus valores por 8:
220/8 = 27,50
120/8 = 15
50/8 = 6,25
Alerta de pegadinha: Veja que a letra B indica exatamente todos esses valores respectivamente, porém estaria errado marcar essa alternativa pois você estaria se esquecendo de que o projetista reduziu 20% dessa escala.
Então agora basta reduzir 20% de cada um desses valores:
100% seria o desenho num todo, logo, desses 100% totais, 20% foram reduzidos, restando 80% do todo, então temos que para a altura do desenho ficaremos com:
27,50cm* 80%
Ou: 27,50cm * 80/100 = 22cm
Veja que a alternativa A já possui esse valor, portanto ela seria a alternativa correta, porém com os outros dois valores ainda teríamos exatamente:
15cm * 80/100 = 12cm e 6,25cm*80/100 = 5cm
Resposta: Letra A
/i.s3.glbimg.com/v1/AUTH_59edd422c0c84a879bd37670ae4f538a/internal_photos/bs/2016/t/S/6QeETSQcCMfhZzB4RCOw/enem2016-138.jpg)
(Clique na imagem para expandir)
138) Essa questão pode embaralhar a cabeça de início se você a ler desatento, mas lendo novamente com calma você constata que se trata apenas de um exercício de conversões de unidades feitas através de regras de três.
Foi informado que o diâmetro dessa roda gigante possui 443 pés (unidade de medida) e o problema quer saber quanto seria esse valor em metros, sendo que no decorrer do enunciado são dados vários dados.
Vamos por partes e realizando nossas regras de três com todas as informações dadas:
Primeiro que 1 pé equivale à 12 polegadas, então a grande pergunta seria... Quantas polegadas dariam em 443 pés?
1 pé ---- 12 polegadas
443 pés ---- x polegadas
x = 443*12 = 5316 polegadas
Então sabemos que 5316 polegadas equivalem ao diâmetro dessa roda gigante na unidade em pés, agora falta usar o mesmo raciocínio com a unidade centímetro:
1 polegada --- 2,54cm
5316 polegadas ---- ycm
y = 2.54*5316 = 13502,64
O problema nos pede a unidade final em metros, e dividindo 13502,64 por 100 (para conversão em metros) teremos aproximadamente 135 metros, logo, a resposta é a letra D.
Resposta: Letra D
/i.s3.glbimg.com/v1/AUTH_59edd422c0c84a879bd37670ae4f538a/internal_photos/bs/2016/2/s/Lfq484SUirf8DVWUjCQQ/enem2016-139.jpg)
(Clique na imagem para expandir)
139) Um problema sobre vazões.
Existe uma fórmula para calcular essas vazões que seria:
Q = V/t ou seja, vazão igual a volume da vazão dividido pelo tempo.
Para a primeira bomba teríamos o seguinte:
Se ela esvaziou 1000 litros em uma hora (como apontado no gráfico), restaram nas outras duas horas 5000 litros, concorda?
Ou seja, essa primeira bomba tem uma vazão de 1000 litros por hora e isso sabemos graças ao gráfico na questão.
As duas bombas por sua vez, esvaziaram os 5000 litros restantes em 2 horas (já que como dito no enunciado, em 3 horas a cisterna estava vazia).
A vazão das duas bombas juntas foi de 5000 litros em duas horas, ou seja, na fórmula teríamos o resultado da vazão de ambas juntas por duas horas:
Q = 5000/2 = 2500
Mas queremos saber a vazão de apenas a segunda bomba!
Se a primeira bomba tem vazão de 1000 litros e as duas juntas tem vazão de 2500 litros, quanto seria a vazão da segunda bomba?
Apenas seria a diferença entre o valor das vazões das bombas juntas (2500) pela vazão da primeira bomba (1000):
2500 - 1000 = 1500
Resposta C
/i.s3.glbimg.com/v1/AUTH_59edd422c0c84a879bd37670ae4f538a/internal_photos/bs/2016/7/R/CXDVkeTaKYSHpvB7N4tg/enem2016-140.jpg)
(Clique na imagem para expandir)
140) O problema nos pede para encontramos o atleta com peso mais regular e o menos regular.
Analisando apenas pelo desvio de peso de todos os atletas, basta ver que o mais regulado é o atleta III, pois possui menos desvio padrão do que os outros (4,08) e o menos regulado é o atleta II, pois possui desvio padrão maior que todos (8,49).
Como o problema nos pede o mais regulado e menos regulado, temos os atletas II e III nessas condições, logo a resposta é a alternativa C que mostra esses valores.
Resposta C
/i.s3.glbimg.com/v1/AUTH_59edd422c0c84a879bd37670ae4f538a/internal_photos/bs/2016/b/6/8zsfLKQTqiO7nqb6HcDg/enem2016-141.jpg)
141) Um problema onde colocaram algumas informações desnecessárias para te confundir!
O que você precisa saber sobre essas medidas de pneu é: que a primeira medida é referente à largura do pneu, ou seja, os primeiros números do código. A segunda informação importante é que o segundo número do pneu é dado através de uma equação.
Essa equação é dada no enunciado, onde diz que ''de'' é igual ao produto de 100 (ou seja, alguma coisa vezes 100) no caso ''esse alguma coisa'' é o que vêm agora: a razão da altura do pneu pela sua largura (a divisão entre eles).
O problema pede para que você analise dentre as opções de códigos apresentadas, qual tem a menor altura.
Para achar a altura referente aos códigos do pneu, basta montarmos aquela equação já dita aqui.
(Vamos chamar a largura de L e a altura de h):
de = 100*h/L
Simplificando temos:
de/100 = h/L ----> de*L/100 = h
Assim deixamos a equação em função da altura que queremos encontrar.
Agora basta irmos substituindo os valores dos códigos na fórmula até acharmos o valor da menor altura.
Primeiro código: 175/65/R/15 (Ignore os valores ''r'' e ''15'', eles servem apenas para atrapalhar!)
Ou seja, temos aqui 175 de largura e o ''de'' valendo 65, substituindo os valores na fórmula teremos:
de*L/100 = h
65*175/100 = h
113,75 = h
Esse código apresenta para a altura do pneu 113,75, mas seria ele o menor?
Vamos ver com os outros:
Segundo código: 175/75/R/15
75*175/100 = 131,25
Terceiro código: 175/80/R/15
75*180/100 = 140
Quarto código: 185/60/R/15
60*185/100 = 111
Último código: 205/55/R/15
55*205/100 = 112,75
Portanto, ao analisar a altura de todos os códigos referentes, o que possui a menor altura é o código: 185/60/R/15
Portanto, resposta E
/i.s3.glbimg.com/v1/AUTH_59edd422c0c84a879bd37670ae4f538a/internal_photos/bs/2016/T/8/VqjaClT7SdDYcyrA4Tyg/enem2016-142.jpg)
142) Uma questão de lógica que se você não numerar com coordenadas cada quadrado, pode ser complicado para resolver.
Eu numerei cada quadrado com as coordenadas (x,y) em ordem crescente em x da esquerda pra direita e em y de baixo pra cima.
Depois eu pintei de rosa os locais apontados no problema: trabalho da mãe, consultório do pai e escola das crianças.
Para saber qual é a distância tanto pela horizontal (coordenada x) quanto pela vertical (coordenada y) dos locais em análise, basta subtrair seus valores correspondentes entre si.
Depois de testar um por um das alternativas, você consta que a localidade 4d é a mais adequada, veja:
Se você subtrair as coordenadas de 4d:
/i.s3.glbimg.com/v1/AUTH_59edd422c0c84a879bd37670ae4f538a/internal_photos/bs/2016/P/z/eOviAFQImODZUoKZoI7Q/enem2016-143.jpg)
143) Questão sobre áreas em geometria plana.
Se o senhor deseja um terreno para o filho com a mesma área que o terreno da figura B, devemos calcular primeiro a área do triângulo da figura B.
Sabendo que para calcular a área de um triângulo temos a fórmula:
b*h/2 (base vezes altura dividido por 2)
Podemos calcular o primeiro triângulo que tem como base 15 e altura 15, também:
15*15/2 = 112,5
O outro triângulo (menor) tem base 3 e a hipotenusa que seria referente ao triângulo como um todo, para esse triângulo torna-se a altura, então: 3*21/2 = 31,5
Somando esses valores: 112,5 + 31,5 = 144
Logo, a área do segundo terreno (figura B) é de 144m².
Sabendo disso... Podemos encontrar x que são as medidas de base e altura do retângulo da figura A.
Sabemos que a área do retângulo pode ser calculada através da fórmula: b*h (base vezes altura), e sabemos também que a área desse retângulo tem de ser igual à área da figura B que é 144.
Aplicando esses valores na fórmula temos que:
A = b*h
144 = x+7(x)
Aplicando a propriedade distributiva no lado direito da igualdade, teremos:
144 = x² + 7x
E passando o 144 pro outro lado da equação ficaremos com:
x² + 7x - 144 = 0
Uma equação de segundo grau.
Resolvendo através de Bhaskara:
delta: 7² - 4 (-144)
delta: 49 + 576
delta = 625
x' = -7 + 25/2
x' = 9
x'' = -7 - 25/2
x'' = -16
Ignorando o fato de a segunda raiz da equação ter dado negativa (pois medidas nunca podem ser negativas) temos as raízes da equação: 9 e 16, ou seja, a alternativa que corresponde a esses valores é a alternativa B.
Resposta B
/i.s3.glbimg.com/v1/AUTH_59edd422c0c84a879bd37670ae4f538a/internal_photos/bs/2016/q/5/haAUKQTFy3qjXMCFoLFQ/enem2016-144.jpg)
144) Aqui vemos um problema relacionado à média aritmética.
Foi dito na questão que foi comprado após 2 meses dessa tabela de lucros uma quantidade de matéria prima equivalente ao mês cujo lucro chegou mais próxima da média de lucros dessa empresa.
O problema quer saber em qual desses meses a compra será realizada.
Para saber disso basta tirarmos a média aritmética desses valores, ou seja, soma-se todos os valores em análise e divide pela quantidade de informações.
Os valores são: 37, 33 ,35, 22, 30, 35, 25
A soma entre esses valores dará: 217
Divida pela quantidade de meses (7): 217/7 = 31
Então a média desses lucros em 7 meses é de 31.
O mês que mais se aproxima da média desses lucros é o quinto mês (V) onde seu lucro é de 30 milhões de reais.
Portanto, a resposta correta é a alternativa D que mostra esse valor.
Resposta D
/i.s3.glbimg.com/v1/AUTH_59edd422c0c84a879bd37670ae4f538a/internal_photos/bs/2016/e/P/NAiHrkS0SApa8rL7vPOg/enem2016-145.jpg)
145) O problema apenas quer que você trabalhe com porcentagem e saiba utilizar as informações fornecidas ao seu favor.
Se o artigo de lei 93 impõe que uma empresa com mais de 1000 funcionários tenha pelo menos 5% deles como sendo reabilitados ou com algum tipo de deficiência, pense... A empresa da questão possui 1200 funcionários, ou seja, está dentro do índice de contratação de funcionários com deficiência em 5%.
Para sabermos quantas pessoas devem ser contratadas ainda, precisamos saber quanto que seria 5% dos 1200 funcionários dessa empresa, ou seja:
5% de 1200 ou
1200*5/100 = 60
Alerta de pegadinha: Marcando a alternativa D que mostra justamente esse valor a questão estaria errada! Pois no problema é dito que já estão empregados nessa empresa 10 funcionários reabilitados ou com deficiência, ou seja, dessas 60 contratações podemos excluir 10 delas, ou seja, ficamos com 50 contratações disponíveis.
Resposta letra E
/i.s3.glbimg.com/v1/AUTH_59edd422c0c84a879bd37670ae4f538a/internal_photos/bs/2016/L/M/eQcoliTRiLkkfY5pqZ1A/enem2016-146.jpg)
146) Preste atenção... se a pessoa comprou 4 caixas de picolés e que cada uma delas possuem 20 picolés, então ao todo essa pessoa tem 4*20 = 80 picolés para vender.
Ainda temos que cada caixa custeou 16 reais, ou seja, com quatro caixas a pessoa gastou um total de 64,00 reais. (16*4 = 64)
A pessoa deseja lucrar 20% a mais de quando lucrou no dia anterior de vendas que lhe rendeu 40,00 reais de lucro, ou seja, para saber quanto essa pessoa lucrará com mais 20%, basta calcularmos quanto seria 20% de lucro de 40, ou seja:
40,00 de 120% ou
40*120/100 = 48,00
Então a pessoa obterá 8,00 reais de lucro com esses 20% a mais. Seu lucro será de 48,00.
Agora o enunciado nos diz que esse lucro veio a partir da diferença entre o valor da venda pelo valor da compra. Como não sabemos o valor da venda, chamaremos de x:
48,00 = x - 64,00
64,00 + 48,00 = x
112,00 = x
A pessoa vendeu 112 reais, mas o problema quer saber quanto será o preço do picolé unitário para esse lucro a mais de 20% e não dos 80 picolés vendidos juntos.
Se ela obteve 112 reais com 80 picolés, quanto ela irá obter com apenas uma unidade?
112,00 ---- 80
y ------- 1
80y = 112,00
y = 112,00/80
y = 1,40
Ou seja, ela irá vender seus 80 picolés por 1,40 cada para obter aqueles 20% de lucro, logo, a alternativa que corresponde a esse valor é a alternativa C.
Resposta C
/i.s3.glbimg.com/v1/AUTH_59edd422c0c84a879bd37670ae4f538a/internal_photos/bs/2016/K/B/GHqlPHRvugAPgMC1A2bg/enem2016-147.jpg)
147) Uma questão sobre análise combinatória, mais precisamente sobre combinações.
Vamos primeiro lembrar a fórmula de combinação para não se perder no problema:
n é a quantidade de elementos a se combinar num todo e p é a quantidade que forma o grupo.
Nessa fórmula, n seria 10 (por se tratar de 10 tenistas ao todo) e p seria a quantidade de jogadores que irão ser combinados, ou seja, 2.
Então aplicando esses valores na fórmula teremos:
Resolvendo o que há em parênteses:
E ainda no problema é nos dito que entre esses tenistas não pode acontecer de 2 deles serem canhotos, ou seja, devemos retirar desse total de combinações, a possibilidade de termos 2 canhotos sorteados na combinação.
Para isso, teremos que calcular a combinação entre esses 4 canhotos impedindo que dois deles caiam juntos, ou seja, uma combinação onde n = 4 (número de canhotos) e p = 2 (quantidade de tenistas sorteados):
Simplificando:
Já que o exercício não nos pede para realizarmos esse cálculo com fatoriais, simplesmente teríamos todas as possibilidades de combinações entre esses 10 tenistas, sorteando 2 deles, menos a possibilidade da combinação ser exatamente entre dois canhotos, ou seja:
Resposta A
/i.s3.glbimg.com/v1/AUTH_59edd422c0c84a879bd37670ae4f538a/internal_photos/bs/2016/8/e/s1C6zuQ6uR6pAElLejFg/enem2016-148.jpg)
148) Essa questão é cheia de pegadinhas, mas se prestarmos bem atenção no enunciado não seremos pegos por ela.
Primeiro vamos montar o esquema de unidades corretamente:
U, D, C, M, DM, CM
(Lendo da direita para a esquerda)
CM, DM, M, C, D, U
Agora basta colocarmos a quantidade de peças indicas na figura em cada unidade correta, seguindo o esquema que acabamos de montar com base do enunciado:
CM = 4
DM = 6
M = 0
C = 1
D = 7
U = 1
Ou seja, 46071
Letra D
/i.s3.glbimg.com/v1/AUTH_59edd422c0c84a879bd37670ae4f538a/internal_photos/bs/2016/O/x/5BovxCRXaAr64VqS5lRw/enem2016-149.jpg)
149) Quando eu li essa questão pela primeira vez eu pensei que iria ter que realizar muitos cálculos, mas se você analisar bem, essa questão só exige que você tenha atenção.
Veja que os projéteis devem se encontrar nesse ponto aqui:
/i.s3.glbimg.com/v1/AUTH_59edd422c0c84a879bd37670ae4f538a/internal_photos/bs/2016/2/y/MKQhDfTA6p4AxEkd7cJQ/enem2016-150.jpg)
150) Questão de lógica.
Vamos analisar as expressões que o enunciado nos dá:
A primeira é que a espessura do revestimento é inversamente proporcional ao quadrado da distância da fonte sonora.
Temos duas expressões para escrevermos, as com incógnitas (que chamaremos de artifício) e a expressão com os termos conhecidos.
Na matemática, ser inversamente proporcional indica multiplicação.
Vamos chamar a espessura do material de E (pois não conhecemos seu valor).
Na expressão teremos:
E1 * D²
E a outra expressão seria:
E2 * 3²
Unindo as expressões teremos o seguinte:
E1 * D² = E2 * 3²
Isolando E2 iremos obter a seguinte equação:
A segunda expressão do enunciado nos diz que o custo é diretamente proporcional ao volume do material.
Diretamente proporcional é uma divisão.
Novamente seguindo o raciocínio da primeira expressão, teremos o artifício e a expressão de termos conhecido.
Chamaremos o volume de V, logo para o artifício teremos:
Para a expressão com os termos conhecidos:
Unificando-as:
Para calcular os volumes (1 e 2) iremos também utilizar o artifício.
O volume pode ser obtido através do produto da área pela espessura do material:
V1 = A * E1
E para V2 teremos:
V2 = 9 * E2
Substituindo esses valores de volume na fórmula ficaremos com:
Sabemos que
Então substituindo esse valor na equação ficaremos assim:
Veja que você pode simplificar 9 e 3²:
E também cancelar E1 dos dois lados da igualdade:
E então temos 'A' que está dividindo passa pro outro lado da equação multiplicando:
Por fim temos a nossa equação finalizada, pois é pedido a expressão em função do custo (C).
A alternativa que se encaixa nessas condições é a alternativa B.
Resposta B
/i.s3.glbimg.com/v1/AUTH_59edd422c0c84a879bd37670ae4f538a/internal_photos/bs/2016/B/V/jv1LsRTvK0uQ8koojaBw/q151.jpg)
151) Veja que a menina na primeira medição tinha 85 cm aos três anos, e na segunda medição com agora 4 anos e 4 meses ela está com 1,05 metros.
Como eu sei disso?
O gráfico irá nos dizer qual será a altura da menina na segunda medição.
O enunciado nos diz que aos 4 anos e 4 meses, ou seja, nessa região aqui do gráfico:
A menina está com altura equivalente a algum ponto da curva p50. A curva p50 é justamente essa aqui:
Veja que se traçarmos uma reta da região correspondente a idade da menina (4 anos e 4 meses) até a curva p50, iremos encontrar exatamente esse ponto aqui:
Este ponto corresponde pelo número 105, ou seja, 1.05 metros.
Se a menina tinha 85 cm e agora tem 1,05 metros, isso significa que ela teve um aumento de 20 cm nesse período: 105 - 80 = 20.
Para calcularmos o aumento percentual, nós iremos obter a razão do aumento pelo seu valor inicial e depois multiplicarmos o resultado por 100.
O aumento foi de 20cm como já vimos, e sua altura inicial era de 85 cm, ou seja:
20/85 = 0,235
Multiplicando esse valor por 100 encontraremos exatamente 23,5.
Ou seja, o aumento percentual da altura da menina nesse intervalo de tempo foi de 23,5%.
Resposta A
/i.s3.glbimg.com/v1/AUTH_59edd422c0c84a879bd37670ae4f538a/internal_photos/bs/2016/i/U/tts1NiQlS59BMx19G84g/q152.jpg)
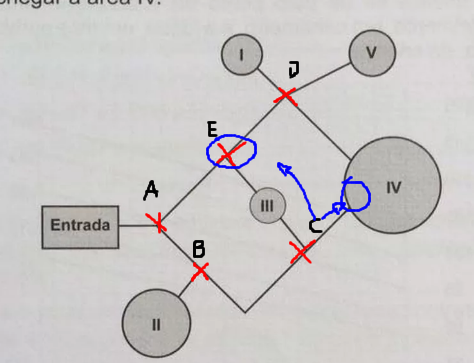
Uma questão interessante de probabilidade.
O enunciado nos estabelece algumas condições para que possamos calcular a probabilidade corretamente:
1) O menino não pode passar por outras áreas além da área de destino (a área IV);
2) O menino não pode retornar às áreas que já passou;
3) Todas os eventos de caminhos prováveis devem acontecer a partir da entrada, não de um caminho aleatório, como dito logo no início da questão.
Ou seja, na hora de contarmos as possibilidades, devemos descartar as possibilidades do garoto voltar num ponto que já passou ou os pontos das outras áreas que não sejam a área de destino.
Vamos analisar os pontos que o menino passará, sendo que cada ponto do mapa deve se conectar a uma área distinta:
Aqui temos demarcados todos os pontos que se conectam com cada área do parque e que o menino terá que passar.
Para ficar mais fácil de acompanhar o raciocínio vamos nomear esses pontos:
Partindo do ponto A (que é o ponto da entrada do parque), se ele for por baixo ele passará pelos caminhos:
A --> B --> C --> IV
Ou por cima, ele fará os caminhos:
A --> E --> D --> IV
Lembrando que com o termo ''ou'' em nossas possibilidades teremos que ao fim somar todas as probabilidades de caminhos, ou seja: (A,B,C) + (A,E,D)
Mas faremos isso mais tarde.
Vamos primeiro estipular as chances de possíveis caminhos.
Começando pelo caminho por baixo.
Se o menino sair do ponto A ele possui dois caminhos: B ou E:
Observe que dessa forma possuímos 1 caminho para duas possibilidades favoráveis, ou seja: 1/2
E ainda temos as outras possibilidades pelo caminho por cima:
Se o menino estiver no ''ponto E'' ele também possuíra dois caminhos a traçar: C e D.
Note que desconsideramos a volta que ele faria para o ponto A pois o enunciado nos impôs a condição de não consideramos a pessoa voltar ao ponto que já passou.
Portanto, para essa situação temos novamente 1/2.
E também ainda pelo caminho de cima temos as possibilidades para o ponto D que serão:
I, V ou IV, ou seja, 3 caminhos: 1/3:
Lembre-se: Por cima temos as possibilidades: 1/2 e 1/2 e 1/3.
O termo ''e'' implica que devemos unir as possibilidades através de uma multiplicação, logo:
1/2 * 1/2 * 1/3 = 1/12
Por baixo temos a possibilidade de o menino sair do ponto A e ir novamente entre o ponto B e o ponto E: 1/2.
No ponto B, o menino pode ir ao ponto A ou ao ponto C, novamente 1/2.
No ponto C o menino pode ir ao ponto E ou ao local IV, também 1/2:
Multiplicando os valores encontrados pelo caminho por baixo teremos:
1/2 * 1/2 * 1/2 = 1/8
Agora temos as possibilidades dos caminhos por cima (1/12) e por baixo (1/8).
Como dito no início da explicação, o termo ''ou'' irá unir essas possibilidades através da soma, logo:
1/12 + 1/8
Ao realizar o MMC de 8 e 12 você encontrará 24.
Veja que a alternativa que leva o 24 no denominador é a alternativa C. Você já poderia marcar essa resposta como a certa, mas se desejar tirar a prova realize a soma das frações e chegue em:
3/24 + 2/24 = 5/24
Resposta C
/i.s3.glbimg.com/v1/AUTH_59edd422c0c84a879bd37670ae4f538a/internal_photos/bs/2016/6/g/koJlFFT9CbFi0csaL9aQ/q153.jpg)
153) Um problema sobre media aritmética.
Podemos saber disso porque na pergunta do enunciado ele diz a seguinte frase: "... cujo número de casos seja menor ou igual à média dos casos confirmados."
A questão então nos dá uma tabela com o número de casos confirmados em cada região do país.
Para tirar sua média basta somar todos esses números e dividir pela quantidade de regiões na tabela.
237 + 262 + 158 + 159 + 160 + 278 + 300 + 278 = 1832
Dividindo pela quantidade de regiões:
1832/8 = 229
Ou seja, a média de casos confirmados em todas as regiões é de 229.
E então o problema nos diz que serão enviados 10 funcionários para cada região que tem a quantidade de casos confirmados maior que a média.
A média é 229, então basta ver as regiões que possuem números maiores a 229, no caso são essas aqui:
Agora basta pensar: Se são 10 funcionários para cada região com casos acima da média, e essas regiões totalizam 5, logo, 50 funcionários serão confirmados para essas 5 áreas.
Depois disso é só perceber que apenas 3 regiões estão abaixo da média de casos confirmados.
O problema nos diz que para cada região abaixo ou igual a média, serão acionados 7 funcionários para cada uma dessas regiões.
7 funcionários para 3 regiões totalizam um total de 21 funcionários.
A questão quer saber quantos funcionários ao todo serão contratos pela prefeitura, ou seja:
50 + 21 = 71
Resposta D
/i.s3.glbimg.com/v1/AUTH_59edd422c0c84a879bd37670ae4f538a/internal_photos/bs/2016/B/w/Sh0UWhQqmeWCTzDAHLgQ/q154.jpg)
154) Em minha opinião essa questão é uma das mais fáceis desse Enem, se trata apenas de uma questão de divisão.
O problema nos dá 5 marcas distintas que mostram a concentração de fibras em seus pães integrais e quer saber qual delas possui a maior concentração em fibras.
Já que foi dito no problema que a concentração de fibras é calculada pela massa de fibra dividido pela massa do pão, basta dividir cada uma dessas marcas e ver qual resultado é o maior:
Marca A-> 2/50 = 0,04
Marca B -> 5/40 = 0,125
Marca C -> 5/100 = 0,05
Marca D -> 6/90 = 0,65
Marca E -> 7/70 = 0,1
Veja que a marca B possui 0,125 em concentração de fibras, logo, é a que mais possui essa concentração dentre as outras marcas.
Alternativa B
/i.s3.glbimg.com/v1/AUTH_59edd422c0c84a879bd37670ae4f538a/internal_photos/bs/2016/9/J/E66BIPQ06CupUhDA66iQ/q155.jpg)
155) Apenas questão de lógica.
Veja, vamos colocar alguns pontos coloridos na cadeira aberta:
Agora imagina esses pontos coloridos se unindo ao fechar a cadeira e pondo-a de lado.
Veja que a parte de cima formaria um retângulo, as parte em amarelo e laranja dariam a impressão de estarem unificadas, bem como as parte em verde, as partes em azul e roxo formariam um quadrado ao fechar esse ''x'':
A alternativa que mais se assemelha a esse desenho é a alternativa C.
Resposta C
/i.s3.glbimg.com/v1/AUTH_59edd422c0c84a879bd37670ae4f538a/internal_photos/bs/2016/Y/l/k6BAguRQAr9IlSvJCKKg/156.jpg)
156) Temos algumas informações dadas no enunciado.
Diz que para cada metro quadrado de área ocupada possuímos uma densidade de 4 pessoas.
O organizador do evento registra que às 10 horas da manhã um quadrado de lados de 500m tem sua área totalmente ocupada.
Ou seja, se para cada metro quadrado a densidade de pessoas é 4 e o quadrado tem 500 metros de lado, basta primeiro sabermos a área desse quadro, ou seja: l² -> 500² = 250000.
Em 25000 metros de área, quanto seria a densidade demográfica dessas pessoas?
250000 * 4 = 1000000
Às 10 da manhã já sabemos que temos 1000000 pessoas presentes no evento.
Depois é informado que à cada hora até o início do evento, a taxa de pessoas aumentará em 120000.
Sabemos que o evento se inicia às 4 horas da tarde (16 horas) e que às 11 horas da manhã já teríamos então mais 120.000 pessoas.
Para saber quantas pessoas teríamos ao todo no início do evento (às 16 horas) basta fazer uma regra de três.
Das 10 da manhã até às 16 horas se passaram 6 horas, ou seja:
Se na primeira hora do aumento de pessoas teremos 120.000 pessoas, quantas teríamos daqui 6 horas?
120.000 --- 1
x ------ 6
x = 120.000 * 6 = 720.000
Então desde às 10 horas até às 16 horas teríamos um total de 1.720.000 pessoas
720.000 do cálculo que acabamos de fazer e aquelas 1000000 que estavam às 10 horas ocupando o quadrado de 500 metros de lado.
É dito no problema que para cada 2000 pessoas se faz necessário um policial.
O problema quer saber, no início do evento quantos policiais serão necessários?
2000 pessoas ------ 1 policial
1.720.000 pessoas ------- y policiais
y = 1720000/2000
y = 860
Resposta E
/i.s3.glbimg.com/v1/AUTH_59edd422c0c84a879bd37670ae4f538a/internal_photos/bs/2016/A/m/Ylu7CLQvCZtovtus0h6w/157.jpg)
157) Outra questão relacionada à média, porém agora um pouco mais elaborada.
Para tirar a média de algo nós somamos todos os valores apresentados e dividimos pela quantidade de informações referentes a esse valor.
Aqui nós temos o caso de um dos valores ser desconhecido, ou seja, no caso, uma incógnita, que é justamente o que queremos encontrar.
Esse é o valor do lucro mínimo da empresa no mês de Junho.
Chamaremos então esse valor de x.
Se numa média nós somamos todos os valores apresentados então faremos o mesmo aqui:
21 + 35 + 21 + 30 + 38 + x
O 'x' ali no caso é o valor do lucro do mês de Junho que não sabemos de quanto que é.
Somando os termos conhecidos ficaremos com:
145 + x
E ainda para retirarmos a média de algo, devemos dividir pela quantidade de informações referentes.
Temos 5 meses apresentados na tabela (de Janeiro à Maio) e ainda como estamos incluindo 'x' na média, temos também que considerar o mês de Junho, ou seja, 6 meses:
145 + x /6
Agora preste atenção no enunciado: Ele nos diz que para o gerente permanecer na empresa, a média de lucros da mesma deva ser no mínimo de 30 mil reais.
Ou seja, nosso objetivo é 30 mil reais, em outras palavras, devemos criar uma equação que satisfaça os 30 mil reais, entende?
Logo, toda essa média que acabamos de fazer (145 + x/6) deva dar exatos 30 mil reais, ou seja:
145 + x/6 = 30
Agora resolvendo a equação, o 6 passa pro outro lado da igualdade multiplicando:
145 + x = 30*6
145 + x = 180
Isolando x:
x = 180 - 145
x = 35
Se x = 35, isso significa que o lucro do próximo mês (Junho) deve ser de no mínimo 35 mil reais, para no final das contas, a média de lucros da empresa ser equivalente a 30 mil reais, assim o gerente permanecerá na empresa.
Apenas conferindo:
21 + 35 + 21 + 30 + 38 + 35/6 = 30
Resposta E
/i.s3.glbimg.com/v1/AUTH_59edd422c0c84a879bd37670ae4f538a/internal_photos/bs/2016/z/C/upB7RPQxWIOaEfrdnRZQ/158.jpg)
158) Esse problema envolve uma função de primeiro grau, pois aqui encontramos um gráfico de uma reta.
A fórmula para uma função de primeiro grau é dada através de:
y = ax + b
Para y e x podemos adotar qualquer ponto que pertence à essa reta.
O ponto (1,30) é um deles, já que suas coordenadas se encontram claras no gráfico.
Temos então para x = 1 e y = 30, logo:
30 = a*1 + b ou
30 = a + b
Como não temos os valores dos coeficientes a e b, devemos estipular um sistema de primeiro grau para encontrar esses valores, ou seja, recorrer a outro ponto da reta.
(6,10) por exemplo, seria uma ótima escolha, pois é agora o único ponto que está descrito com clareza no gráfico.
Para x = 6 e y = 10, ou seja:
10 = a*6 + b ou
10 = 6a + b
Nosso sistema então fica como sendo:
30 = a + b
10 = 6a + b
Podemos isolar 'b' na primeira equação, veja:
30 = a + b
-b = -30 + a * (-1)
b = 30 - a
Substituindo 'b' na segunda equação, podemos encontrar o valor de 'a':
10 = 6a + b
10 = 6a + 30 - a
10 = 5a + 30
10 - 30 = 5a
-20 = 5a
-20/5 = a
-4 = a
Então temos que a = -4
Para encontrarmos o valor de 'b' basta substituir 'a' em qualquer uma das equações por -4:
30 = a + b
30 = -4 + b
30 + 4 = b
34 = b
Por fim, temos que nossa função (agora com os coeficientes 'a' e 'b' conhecidos) fica como sendo:
f(x) = -4x + 34
O que queremos encontrar é 'x', ou seja, no gráfico através da coordenada x, onde será o ponto da reta que irá resultar em 0% de capacidade, ou seja, quando o reservatório estiver esvaziado por completo.
A capacidade do reservatório está em função de y no gráfico, ou seja, a equação deve ficar:
y = -4x + 34
0 = -4x + 34
4x = 34
x = 34/4
x = 8,5
Ou seja, se prolongarmos o gráfico dessa reta, teríamos mais ou menos o seguinte:
Logo, após o sexto mês, o reservatório se encontraria vazio quase no nono mês, na metade do oitavo mês para ser mais exata.
Ou seja, se passariam 2 meses e meio para que isso acontecesse: 8,5 - 6 = 2,5
Resposta A
/i.s3.glbimg.com/v1/AUTH_59edd422c0c84a879bd37670ae4f538a/internal_photos/bs/2016/6/o/REJ7A7Tdmd9R6EA8sfiQ/159.jpg)
159) Outra questão de média.
Tirando a média de vacinas aplicadas, teremos:
21 + 22 + 25 + 31 + 21/5 = 24
O estoque dos próximos meses, como dito no problema, deve ser igual à média de vacinadas aplicadas vezes 12:
estoque = 24 * 12
estoque = 288
Alerta de pegadinha: Porém, esse seria o estoque se o mesmo estivesse vazio desde o primeiro mês.
Se marcar a alternativa E você estaria errando!
Lembre-se que no primeiro mês haviam 228 vacinas e o posto utilizou 120 vacinas (vide a quantidade de vacinas aplicadas).
Então dessas 228 vacinas, 120 foram usadas, ou seja, restaram 108 vacinas.
Então o estoque deve ser a quantidade total de vacinas que encontramos, menos a quantidade de vacinas que já temos:
288 - 108 = 180
Resposta B
/i.s3.glbimg.com/v1/AUTH_59edd422c0c84a879bd37670ae4f538a/internal_photos/bs/2016/b/4/tzOziXR3uucJBM2AkPaQ/160.jpg)
160) Essa questão de logaritmos pode ser difícil se você não conhecer a lei do resfriamento de Newton, cuja a fórmula se dá por:
T seria a temperatura final
Ta seria a temperatura ambiente
T0 seria a temperatura inicial
'e' seria a constante de resfriamento
kt seria o tempo de resfriamento.
Como não foi dado no problema a temperatura ambiente, podemos descartar Ta na equação, ficaremos com:
Veja que a temperatura final da liga é de 30 ºC, bem como a temperatura inicial é de 3000 ºC.
Substituindo esses valores na fórmula teremos o seguinte:
A constante de resfriamento é aquele 1% que a liga metálica resfria à cada meia hora.
Se à cada meia hora é resfriado 1% de um todo (que costuma ser 100%) isso significa que teremos 99% do todo na primeira meia hora:
Dizer que algo está à 99% é o mesmo que dizer 99/100. Trabalharemos com decimais para facilitar o cálculo:
Como à cada meia hora o metal resfria 1%, podemos dizer que temos 2 tempos de meia hora para dar uma hora ao todo. (Já que o enunciado pede o tempo em hora, não em minuto).
Então:
Você pode passar o 3000 que está multiplicando 99/100 pro outro lado da igualdade, dividindo:
Simplificando 30 e 3000 você ficará com:
E ainda simplificando 3/300 por 3, teremos:
Já que temos uma incógnita no expoente de uma potência, podemos aplicar logaritmo dos dois lados da igualdade:
Agora que temos log de ambos lados da equação podemos utilizar as propriedades operatórias dos logaritmos para resolver essa equação.
A primeira propriedade nos diz que se tivermos logaritmos de mesma base dividindo, podemos subtraí-los, então:

Nesse momento podemos resolver os logaritmos:
Log de 1 = 0
Log de 100 = 2
Log de 99 teremos:
99 | 3
33 | 3
11 | 11
1
Ou seja:
Log99 = Log3² * Log11
Outra propriedade dos logaritmos nos diz que se ambos logs tiverem mesma base e estiverem multiplicando, podemos somá-los:
log99 = log3² + log11
Então teremos por fim:
-2 = log3² + log11 - 2²t
Outra propriedade nos diz que o expoente de um log pode multiplicar seu logaritmando:
-2 = 2t(2*log3 + log 11 - 2)
O enunciado nos diz que log 3 = 0,477 e log 11 = 1,041 então temos que:
-2 = 2t(2*0,477 + 1,041 - 2)
Resolvendo:
-2 = 2t * -0,005
-2 = -0,01t
/i.s3.glbimg.com/v1/AUTH_59edd422c0c84a879bd37670ae4f538a/internal_photos/bs/2016/M/O/dAlo0fQPiGPmjHgGN5HQ/enem2016-136.jpg)
(Clique na imagem para expandir)
136) Aqui temos um problema muito corriqueiro de cálculos envolvendo a geometria espacial.
No caso, o sólido seria um silo de grãos que é formado por um cilindro com um cone pelo topo.
O problema foi tão bondoso que deixou de graça todas as medidas de ambos sólidos: alturas e raio da circunferência!
A questão quer saber quantas viagens um caminhão que suporta apenas 20m³ de carga teria que fazer para carregar todo o grão suportado pelo volume total do silo.
Para saber disso, basta apenas calcularmos o volume do silo que seria o volume de seu cilindro (V1) e de seu cone (V2):
Calculando volume do cilindro:
V1 = AB * h
Como se trata de um cilindro, seu volume em AB é dado por pi r², então:
V1 = 3 * 3² * 12 = 324
Calculando volume do cone que tem como fórmula:
V2 = AB*h/3 ou seja:
V2 = 3*3²*3/3 = 27
O silo é a soma do volume do cone com o volume do cilindro (V1 e V2) então temos que V1 + V2 = 351
Se o caminhão capacita até 20m³ de carga, quantas viagens ele faria para suportar 351m³ de carga?
Basta aplicar uma regra de três para resolver:
20 --- 1 viagem
351 --- x viagens;
20x = 351
x = 351/20 = 17,55
Alerta de pegadinha: Marcando a letra C (17 viagens) você estaria errando, pois o resultado não deu 17 viagens exatas, mas sim 17.55, portanto a resposta certa é a D: 18 viagens!!!!
Resposta: Letra D
/i.s3.glbimg.com/v1/AUTH_59edd422c0c84a879bd37670ae4f538a/internal_photos/bs/2016/b/P/w02EcjRLeoaWE9ll8hiw/enem2016-137.jpg)
(Clique na imagem para expandir)
137) É um problema de escala.
Foram dadas as dimensões do guarda-roupa: 220cm altura, 120cm largura e 50cm de profundidade como dito no problema.
Esse guarda-roupas foi projetado numa escala de 1 para 8 (1:8) e mesmo assim não coube na folha para impressão, e tendo isso como problema, seu projetista ajustou a impressão para diminuir 20% do tamanho do desenho, e então o problema pergunta, depois dessa redução... Quanto passou a ser as dimensões projetadas deste guarda-roupas?
Se temos uma escala de 1:8 em todas as dimensões reais do objeto, então para saber as dimensões projetadas basta dividir todos seus valores por 8:
220/8 = 27,50
120/8 = 15
50/8 = 6,25
Alerta de pegadinha: Veja que a letra B indica exatamente todos esses valores respectivamente, porém estaria errado marcar essa alternativa pois você estaria se esquecendo de que o projetista reduziu 20% dessa escala.
Então agora basta reduzir 20% de cada um desses valores:
100% seria o desenho num todo, logo, desses 100% totais, 20% foram reduzidos, restando 80% do todo, então temos que para a altura do desenho ficaremos com:
27,50cm* 80%
Ou: 27,50cm * 80/100 = 22cm
Veja que a alternativa A já possui esse valor, portanto ela seria a alternativa correta, porém com os outros dois valores ainda teríamos exatamente:
15cm * 80/100 = 12cm e 6,25cm*80/100 = 5cm
Resposta: Letra A
/i.s3.glbimg.com/v1/AUTH_59edd422c0c84a879bd37670ae4f538a/internal_photos/bs/2016/t/S/6QeETSQcCMfhZzB4RCOw/enem2016-138.jpg)
(Clique na imagem para expandir)
138) Essa questão pode embaralhar a cabeça de início se você a ler desatento, mas lendo novamente com calma você constata que se trata apenas de um exercício de conversões de unidades feitas através de regras de três.
Foi informado que o diâmetro dessa roda gigante possui 443 pés (unidade de medida) e o problema quer saber quanto seria esse valor em metros, sendo que no decorrer do enunciado são dados vários dados.
Vamos por partes e realizando nossas regras de três com todas as informações dadas:
Primeiro que 1 pé equivale à 12 polegadas, então a grande pergunta seria... Quantas polegadas dariam em 443 pés?
1 pé ---- 12 polegadas
443 pés ---- x polegadas
x = 443*12 = 5316 polegadas
Então sabemos que 5316 polegadas equivalem ao diâmetro dessa roda gigante na unidade em pés, agora falta usar o mesmo raciocínio com a unidade centímetro:
1 polegada --- 2,54cm
5316 polegadas ---- ycm
y = 2.54*5316 = 13502,64
O problema nos pede a unidade final em metros, e dividindo 13502,64 por 100 (para conversão em metros) teremos aproximadamente 135 metros, logo, a resposta é a letra D.
Resposta: Letra D
/i.s3.glbimg.com/v1/AUTH_59edd422c0c84a879bd37670ae4f538a/internal_photos/bs/2016/2/s/Lfq484SUirf8DVWUjCQQ/enem2016-139.jpg)
(Clique na imagem para expandir)
139) Um problema sobre vazões.
Existe uma fórmula para calcular essas vazões que seria:
Q = V/t ou seja, vazão igual a volume da vazão dividido pelo tempo.
Para a primeira bomba teríamos o seguinte:
Se ela esvaziou 1000 litros em uma hora (como apontado no gráfico), restaram nas outras duas horas 5000 litros, concorda?
Ou seja, essa primeira bomba tem uma vazão de 1000 litros por hora e isso sabemos graças ao gráfico na questão.
As duas bombas por sua vez, esvaziaram os 5000 litros restantes em 2 horas (já que como dito no enunciado, em 3 horas a cisterna estava vazia).
A vazão das duas bombas juntas foi de 5000 litros em duas horas, ou seja, na fórmula teríamos o resultado da vazão de ambas juntas por duas horas:
Q = 5000/2 = 2500
Mas queremos saber a vazão de apenas a segunda bomba!
Se a primeira bomba tem vazão de 1000 litros e as duas juntas tem vazão de 2500 litros, quanto seria a vazão da segunda bomba?
Apenas seria a diferença entre o valor das vazões das bombas juntas (2500) pela vazão da primeira bomba (1000):
2500 - 1000 = 1500
Resposta C
/i.s3.glbimg.com/v1/AUTH_59edd422c0c84a879bd37670ae4f538a/internal_photos/bs/2016/7/R/CXDVkeTaKYSHpvB7N4tg/enem2016-140.jpg)
(Clique na imagem para expandir)
140) O problema nos pede para encontramos o atleta com peso mais regular e o menos regular.
Analisando apenas pelo desvio de peso de todos os atletas, basta ver que o mais regulado é o atleta III, pois possui menos desvio padrão do que os outros (4,08) e o menos regulado é o atleta II, pois possui desvio padrão maior que todos (8,49).
Como o problema nos pede o mais regulado e menos regulado, temos os atletas II e III nessas condições, logo a resposta é a alternativa C que mostra esses valores.
Resposta C
/i.s3.glbimg.com/v1/AUTH_59edd422c0c84a879bd37670ae4f538a/internal_photos/bs/2016/b/6/8zsfLKQTqiO7nqb6HcDg/enem2016-141.jpg)
141) Um problema onde colocaram algumas informações desnecessárias para te confundir!
O que você precisa saber sobre essas medidas de pneu é: que a primeira medida é referente à largura do pneu, ou seja, os primeiros números do código. A segunda informação importante é que o segundo número do pneu é dado através de uma equação.
Essa equação é dada no enunciado, onde diz que ''de'' é igual ao produto de 100 (ou seja, alguma coisa vezes 100) no caso ''esse alguma coisa'' é o que vêm agora: a razão da altura do pneu pela sua largura (a divisão entre eles).
O problema pede para que você analise dentre as opções de códigos apresentadas, qual tem a menor altura.
Para achar a altura referente aos códigos do pneu, basta montarmos aquela equação já dita aqui.
(Vamos chamar a largura de L e a altura de h):
de = 100*h/L
Simplificando temos:
de/100 = h/L ----> de*L/100 = h
Assim deixamos a equação em função da altura que queremos encontrar.
Agora basta irmos substituindo os valores dos códigos na fórmula até acharmos o valor da menor altura.
Primeiro código: 175/65/R/15 (Ignore os valores ''r'' e ''15'', eles servem apenas para atrapalhar!)
Ou seja, temos aqui 175 de largura e o ''de'' valendo 65, substituindo os valores na fórmula teremos:
de*L/100 = h
65*175/100 = h
113,75 = h
Esse código apresenta para a altura do pneu 113,75, mas seria ele o menor?
Vamos ver com os outros:
Segundo código: 175/75/R/15
75*175/100 = 131,25
Terceiro código: 175/80/R/15
75*180/100 = 140
Quarto código: 185/60/R/15
60*185/100 = 111
Último código: 205/55/R/15
55*205/100 = 112,75
Portanto, ao analisar a altura de todos os códigos referentes, o que possui a menor altura é o código: 185/60/R/15
Portanto, resposta E
/i.s3.glbimg.com/v1/AUTH_59edd422c0c84a879bd37670ae4f538a/internal_photos/bs/2016/T/8/VqjaClT7SdDYcyrA4Tyg/enem2016-142.jpg)
142) Uma questão de lógica que se você não numerar com coordenadas cada quadrado, pode ser complicado para resolver.
Eu numerei cada quadrado com as coordenadas (x,y) em ordem crescente em x da esquerda pra direita e em y de baixo pra cima.
Depois eu pintei de rosa os locais apontados no problema: trabalho da mãe, consultório do pai e escola das crianças.
Para saber qual é a distância tanto pela horizontal (coordenada x) quanto pela vertical (coordenada y) dos locais em análise, basta subtrair seus valores correspondentes entre si.
Depois de testar um por um das alternativas, você consta que a localidade 4d é a mais adequada, veja:
Se você subtrair as coordenadas de 4d:
Verá que as distâncias (x,y) desse ponto até o ponto (5,2) que é o trabalho da mãe será de (2,1)
Do ponto (1,2) que é o consultório do pai, também será (2,1)
E do ponto (3,6) que é a escola, será de 0,3 (a distância que vai ser mais próxima dentre esses dois pontos entre todas as alternativas).
Então por isso, a resposta é a letra C
/i.s3.glbimg.com/v1/AUTH_59edd422c0c84a879bd37670ae4f538a/internal_photos/bs/2016/P/z/eOviAFQImODZUoKZoI7Q/enem2016-143.jpg)
143) Questão sobre áreas em geometria plana.
Se o senhor deseja um terreno para o filho com a mesma área que o terreno da figura B, devemos calcular primeiro a área do triângulo da figura B.
Sabendo que para calcular a área de um triângulo temos a fórmula:
b*h/2 (base vezes altura dividido por 2)
Podemos calcular o primeiro triângulo que tem como base 15 e altura 15, também:
15*15/2 = 112,5
O outro triângulo (menor) tem base 3 e a hipotenusa que seria referente ao triângulo como um todo, para esse triângulo torna-se a altura, então: 3*21/2 = 31,5
Somando esses valores: 112,5 + 31,5 = 144
Logo, a área do segundo terreno (figura B) é de 144m².
Sabendo disso... Podemos encontrar x que são as medidas de base e altura do retângulo da figura A.
Sabemos que a área do retângulo pode ser calculada através da fórmula: b*h (base vezes altura), e sabemos também que a área desse retângulo tem de ser igual à área da figura B que é 144.
Aplicando esses valores na fórmula temos que:
A = b*h
144 = x+7(x)
Aplicando a propriedade distributiva no lado direito da igualdade, teremos:
144 = x² + 7x
E passando o 144 pro outro lado da equação ficaremos com:
x² + 7x - 144 = 0
Uma equação de segundo grau.
Resolvendo através de Bhaskara:
delta: 7² - 4 (-144)
delta: 49 + 576
delta = 625
x' = -7 + 25/2
x' = 9
x'' = -7 - 25/2
x'' = -16
Ignorando o fato de a segunda raiz da equação ter dado negativa (pois medidas nunca podem ser negativas) temos as raízes da equação: 9 e 16, ou seja, a alternativa que corresponde a esses valores é a alternativa B.
Resposta B
/i.s3.glbimg.com/v1/AUTH_59edd422c0c84a879bd37670ae4f538a/internal_photos/bs/2016/q/5/haAUKQTFy3qjXMCFoLFQ/enem2016-144.jpg)
144) Aqui vemos um problema relacionado à média aritmética.
Foi dito na questão que foi comprado após 2 meses dessa tabela de lucros uma quantidade de matéria prima equivalente ao mês cujo lucro chegou mais próxima da média de lucros dessa empresa.
O problema quer saber em qual desses meses a compra será realizada.
Para saber disso basta tirarmos a média aritmética desses valores, ou seja, soma-se todos os valores em análise e divide pela quantidade de informações.
Os valores são: 37, 33 ,35, 22, 30, 35, 25
A soma entre esses valores dará: 217
Divida pela quantidade de meses (7): 217/7 = 31
Então a média desses lucros em 7 meses é de 31.
O mês que mais se aproxima da média desses lucros é o quinto mês (V) onde seu lucro é de 30 milhões de reais.
Portanto, a resposta correta é a alternativa D que mostra esse valor.
Resposta D
/i.s3.glbimg.com/v1/AUTH_59edd422c0c84a879bd37670ae4f538a/internal_photos/bs/2016/e/P/NAiHrkS0SApa8rL7vPOg/enem2016-145.jpg)
145) O problema apenas quer que você trabalhe com porcentagem e saiba utilizar as informações fornecidas ao seu favor.
Se o artigo de lei 93 impõe que uma empresa com mais de 1000 funcionários tenha pelo menos 5% deles como sendo reabilitados ou com algum tipo de deficiência, pense... A empresa da questão possui 1200 funcionários, ou seja, está dentro do índice de contratação de funcionários com deficiência em 5%.
Para sabermos quantas pessoas devem ser contratadas ainda, precisamos saber quanto que seria 5% dos 1200 funcionários dessa empresa, ou seja:
5% de 1200 ou
1200*5/100 = 60
Alerta de pegadinha: Marcando a alternativa D que mostra justamente esse valor a questão estaria errada! Pois no problema é dito que já estão empregados nessa empresa 10 funcionários reabilitados ou com deficiência, ou seja, dessas 60 contratações podemos excluir 10 delas, ou seja, ficamos com 50 contratações disponíveis.
Resposta letra E
/i.s3.glbimg.com/v1/AUTH_59edd422c0c84a879bd37670ae4f538a/internal_photos/bs/2016/L/M/eQcoliTRiLkkfY5pqZ1A/enem2016-146.jpg)
146) Preste atenção... se a pessoa comprou 4 caixas de picolés e que cada uma delas possuem 20 picolés, então ao todo essa pessoa tem 4*20 = 80 picolés para vender.
Ainda temos que cada caixa custeou 16 reais, ou seja, com quatro caixas a pessoa gastou um total de 64,00 reais. (16*4 = 64)
A pessoa deseja lucrar 20% a mais de quando lucrou no dia anterior de vendas que lhe rendeu 40,00 reais de lucro, ou seja, para saber quanto essa pessoa lucrará com mais 20%, basta calcularmos quanto seria 20% de lucro de 40, ou seja:
40,00 de 120% ou
40*120/100 = 48,00
Então a pessoa obterá 8,00 reais de lucro com esses 20% a mais. Seu lucro será de 48,00.
Agora o enunciado nos diz que esse lucro veio a partir da diferença entre o valor da venda pelo valor da compra. Como não sabemos o valor da venda, chamaremos de x:
48,00 = x - 64,00
64,00 + 48,00 = x
112,00 = x
A pessoa vendeu 112 reais, mas o problema quer saber quanto será o preço do picolé unitário para esse lucro a mais de 20% e não dos 80 picolés vendidos juntos.
Se ela obteve 112 reais com 80 picolés, quanto ela irá obter com apenas uma unidade?
112,00 ---- 80
y ------- 1
80y = 112,00
y = 112,00/80
y = 1,40
Ou seja, ela irá vender seus 80 picolés por 1,40 cada para obter aqueles 20% de lucro, logo, a alternativa que corresponde a esse valor é a alternativa C.
Resposta C
/i.s3.glbimg.com/v1/AUTH_59edd422c0c84a879bd37670ae4f538a/internal_photos/bs/2016/K/B/GHqlPHRvugAPgMC1A2bg/enem2016-147.jpg)
147) Uma questão sobre análise combinatória, mais precisamente sobre combinações.
Vamos primeiro lembrar a fórmula de combinação para não se perder no problema:
n é a quantidade de elementos a se combinar num todo e p é a quantidade que forma o grupo.
Nessa fórmula, n seria 10 (por se tratar de 10 tenistas ao todo) e p seria a quantidade de jogadores que irão ser combinados, ou seja, 2.
Então aplicando esses valores na fórmula teremos:
Resolvendo o que há em parênteses:
E ainda no problema é nos dito que entre esses tenistas não pode acontecer de 2 deles serem canhotos, ou seja, devemos retirar desse total de combinações, a possibilidade de termos 2 canhotos sorteados na combinação.
Para isso, teremos que calcular a combinação entre esses 4 canhotos impedindo que dois deles caiam juntos, ou seja, uma combinação onde n = 4 (número de canhotos) e p = 2 (quantidade de tenistas sorteados):
Simplificando:
Já que o exercício não nos pede para realizarmos esse cálculo com fatoriais, simplesmente teríamos todas as possibilidades de combinações entre esses 10 tenistas, sorteando 2 deles, menos a possibilidade da combinação ser exatamente entre dois canhotos, ou seja:
Resposta A
/i.s3.glbimg.com/v1/AUTH_59edd422c0c84a879bd37670ae4f538a/internal_photos/bs/2016/8/e/s1C6zuQ6uR6pAElLejFg/enem2016-148.jpg)
148) Essa questão é cheia de pegadinhas, mas se prestarmos bem atenção no enunciado não seremos pegos por ela.
Primeiro vamos montar o esquema de unidades corretamente:
U, D, C, M, DM, CM
(Lendo da direita para a esquerda)
CM, DM, M, C, D, U
Agora basta colocarmos a quantidade de peças indicas na figura em cada unidade correta, seguindo o esquema que acabamos de montar com base do enunciado:
CM = 4
DM = 6
M = 0
C = 1
D = 7
U = 1
Ou seja, 46071
Letra D
/i.s3.glbimg.com/v1/AUTH_59edd422c0c84a879bd37670ae4f538a/internal_photos/bs/2016/O/x/5BovxCRXaAr64VqS5lRw/enem2016-149.jpg)
149) Quando eu li essa questão pela primeira vez eu pensei que iria ter que realizar muitos cálculos, mas se você analisar bem, essa questão só exige que você tenha atenção.
Veja que os projéteis devem se encontrar nesse ponto aqui:
Pois no enunciado é dito que eles devem se interceptar quando o projétil A alcance sua altura máxima, e através da parábola nós podemos constatar que esse ponto é a altura máxima que o projétil A poderá alcançar.
Através do gráfico vemos que os projéteis se encontram nas coordenadas (6,12)
O problema nos pergunta para quanto deverá ser ajustado o coeficiente angular do projétil B para que eles se encontrem.
A fórmula para essa questão é simplesmente a diferença entre o ponto almejado pelo ponto interceptado:
O ponto almejado é (4,16)
O ponto de interceptação é (6,12)
Para abcissa temos: 4 - 6 = -2
Para ordenada temos: 16 - 12 = 4
Para o coeficiente angular temos:
CA = -2 + 4 = 2
Ou seja, 2 positivo, portanto o coeficiente angular deverá aumentar em 2 unidades para os projéteis se encontrarem no ponto (4,16).
Letra C
/i.s3.glbimg.com/v1/AUTH_59edd422c0c84a879bd37670ae4f538a/internal_photos/bs/2016/2/y/MKQhDfTA6p4AxEkd7cJQ/enem2016-150.jpg)
150) Questão de lógica.
Vamos analisar as expressões que o enunciado nos dá:
A primeira é que a espessura do revestimento é inversamente proporcional ao quadrado da distância da fonte sonora.
Temos duas expressões para escrevermos, as com incógnitas (que chamaremos de artifício) e a expressão com os termos conhecidos.
Na matemática, ser inversamente proporcional indica multiplicação.
Vamos chamar a espessura do material de E (pois não conhecemos seu valor).
Na expressão teremos:
E1 * D²
E a outra expressão seria:
E2 * 3²
Unindo as expressões teremos o seguinte:
E1 * D² = E2 * 3²
Isolando E2 iremos obter a seguinte equação:
A segunda expressão do enunciado nos diz que o custo é diretamente proporcional ao volume do material.
Diretamente proporcional é uma divisão.
Novamente seguindo o raciocínio da primeira expressão, teremos o artifício e a expressão de termos conhecido.
Chamaremos o volume de V, logo para o artifício teremos:
Para a expressão com os termos conhecidos:
Unificando-as:
Para calcular os volumes (1 e 2) iremos também utilizar o artifício.
O volume pode ser obtido através do produto da área pela espessura do material:
V1 = A * E1
E para V2 teremos:
V2 = 9 * E2
Substituindo esses valores de volume na fórmula ficaremos com:
Sabemos que

Então substituindo esse valor na equação ficaremos assim:
E então temos 'A' que está dividindo passa pro outro lado da equação multiplicando:
A alternativa que se encaixa nessas condições é a alternativa B.
Resposta B
/i.s3.glbimg.com/v1/AUTH_59edd422c0c84a879bd37670ae4f538a/internal_photos/bs/2016/B/V/jv1LsRTvK0uQ8koojaBw/q151.jpg)
151) Veja que a menina na primeira medição tinha 85 cm aos três anos, e na segunda medição com agora 4 anos e 4 meses ela está com 1,05 metros.
Como eu sei disso?
O gráfico irá nos dizer qual será a altura da menina na segunda medição.
O enunciado nos diz que aos 4 anos e 4 meses, ou seja, nessa região aqui do gráfico:
A menina está com altura equivalente a algum ponto da curva p50. A curva p50 é justamente essa aqui:
Veja que se traçarmos uma reta da região correspondente a idade da menina (4 anos e 4 meses) até a curva p50, iremos encontrar exatamente esse ponto aqui:
Este ponto corresponde pelo número 105, ou seja, 1.05 metros.
Se a menina tinha 85 cm e agora tem 1,05 metros, isso significa que ela teve um aumento de 20 cm nesse período: 105 - 80 = 20.
Para calcularmos o aumento percentual, nós iremos obter a razão do aumento pelo seu valor inicial e depois multiplicarmos o resultado por 100.
O aumento foi de 20cm como já vimos, e sua altura inicial era de 85 cm, ou seja:
20/85 = 0,235
Multiplicando esse valor por 100 encontraremos exatamente 23,5.
Ou seja, o aumento percentual da altura da menina nesse intervalo de tempo foi de 23,5%.
Resposta A
/i.s3.glbimg.com/v1/AUTH_59edd422c0c84a879bd37670ae4f538a/internal_photos/bs/2016/i/U/tts1NiQlS59BMx19G84g/q152.jpg)
Uma questão interessante de probabilidade.
O enunciado nos estabelece algumas condições para que possamos calcular a probabilidade corretamente:
1) O menino não pode passar por outras áreas além da área de destino (a área IV);
2) O menino não pode retornar às áreas que já passou;
3) Todas os eventos de caminhos prováveis devem acontecer a partir da entrada, não de um caminho aleatório, como dito logo no início da questão.
Ou seja, na hora de contarmos as possibilidades, devemos descartar as possibilidades do garoto voltar num ponto que já passou ou os pontos das outras áreas que não sejam a área de destino.
Vamos analisar os pontos que o menino passará, sendo que cada ponto do mapa deve se conectar a uma área distinta:
Aqui temos demarcados todos os pontos que se conectam com cada área do parque e que o menino terá que passar.
Para ficar mais fácil de acompanhar o raciocínio vamos nomear esses pontos:
Partindo do ponto A (que é o ponto da entrada do parque), se ele for por baixo ele passará pelos caminhos:
A --> B --> C --> IV
Ou por cima, ele fará os caminhos:
A --> E --> D --> IV
Lembrando que com o termo ''ou'' em nossas possibilidades teremos que ao fim somar todas as probabilidades de caminhos, ou seja: (A,B,C) + (A,E,D)
Mas faremos isso mais tarde.
Vamos primeiro estipular as chances de possíveis caminhos.
Começando pelo caminho por baixo.
Se o menino sair do ponto A ele possui dois caminhos: B ou E:
Observe que dessa forma possuímos 1 caminho para duas possibilidades favoráveis, ou seja: 1/2
E ainda temos as outras possibilidades pelo caminho por cima:
Se o menino estiver no ''ponto E'' ele também possuíra dois caminhos a traçar: C e D.
Note que desconsideramos a volta que ele faria para o ponto A pois o enunciado nos impôs a condição de não consideramos a pessoa voltar ao ponto que já passou.
Portanto, para essa situação temos novamente 1/2.
E também ainda pelo caminho de cima temos as possibilidades para o ponto D que serão:
I, V ou IV, ou seja, 3 caminhos: 1/3:
Lembre-se: Por cima temos as possibilidades: 1/2 e 1/2 e 1/3.
O termo ''e'' implica que devemos unir as possibilidades através de uma multiplicação, logo:
1/2 * 1/2 * 1/3 = 1/12
Por baixo temos a possibilidade de o menino sair do ponto A e ir novamente entre o ponto B e o ponto E: 1/2.
No ponto B, o menino pode ir ao ponto A ou ao ponto C, novamente 1/2.
No ponto C o menino pode ir ao ponto E ou ao local IV, também 1/2:
Multiplicando os valores encontrados pelo caminho por baixo teremos:
1/2 * 1/2 * 1/2 = 1/8
Agora temos as possibilidades dos caminhos por cima (1/12) e por baixo (1/8).
Como dito no início da explicação, o termo ''ou'' irá unir essas possibilidades através da soma, logo:
1/12 + 1/8
Ao realizar o MMC de 8 e 12 você encontrará 24.
Veja que a alternativa que leva o 24 no denominador é a alternativa C. Você já poderia marcar essa resposta como a certa, mas se desejar tirar a prova realize a soma das frações e chegue em:
3/24 + 2/24 = 5/24
Resposta C
/i.s3.glbimg.com/v1/AUTH_59edd422c0c84a879bd37670ae4f538a/internal_photos/bs/2016/6/g/koJlFFT9CbFi0csaL9aQ/q153.jpg)
153) Um problema sobre media aritmética.
Podemos saber disso porque na pergunta do enunciado ele diz a seguinte frase: "... cujo número de casos seja menor ou igual à média dos casos confirmados."
A questão então nos dá uma tabela com o número de casos confirmados em cada região do país.
Para tirar sua média basta somar todos esses números e dividir pela quantidade de regiões na tabela.
237 + 262 + 158 + 159 + 160 + 278 + 300 + 278 = 1832
Dividindo pela quantidade de regiões:
1832/8 = 229
Ou seja, a média de casos confirmados em todas as regiões é de 229.
E então o problema nos diz que serão enviados 10 funcionários para cada região que tem a quantidade de casos confirmados maior que a média.
A média é 229, então basta ver as regiões que possuem números maiores a 229, no caso são essas aqui:
Agora basta pensar: Se são 10 funcionários para cada região com casos acima da média, e essas regiões totalizam 5, logo, 50 funcionários serão confirmados para essas 5 áreas.
Depois disso é só perceber que apenas 3 regiões estão abaixo da média de casos confirmados.
O problema nos diz que para cada região abaixo ou igual a média, serão acionados 7 funcionários para cada uma dessas regiões.
7 funcionários para 3 regiões totalizam um total de 21 funcionários.
A questão quer saber quantos funcionários ao todo serão contratos pela prefeitura, ou seja:
50 + 21 = 71
Resposta D
/i.s3.glbimg.com/v1/AUTH_59edd422c0c84a879bd37670ae4f538a/internal_photos/bs/2016/B/w/Sh0UWhQqmeWCTzDAHLgQ/q154.jpg)
154) Em minha opinião essa questão é uma das mais fáceis desse Enem, se trata apenas de uma questão de divisão.
O problema nos dá 5 marcas distintas que mostram a concentração de fibras em seus pães integrais e quer saber qual delas possui a maior concentração em fibras.
Já que foi dito no problema que a concentração de fibras é calculada pela massa de fibra dividido pela massa do pão, basta dividir cada uma dessas marcas e ver qual resultado é o maior:
Marca A-> 2/50 = 0,04
Marca B -> 5/40 = 0,125
Marca C -> 5/100 = 0,05
Marca D -> 6/90 = 0,65
Marca E -> 7/70 = 0,1
Veja que a marca B possui 0,125 em concentração de fibras, logo, é a que mais possui essa concentração dentre as outras marcas.
Alternativa B
/i.s3.glbimg.com/v1/AUTH_59edd422c0c84a879bd37670ae4f538a/internal_photos/bs/2016/9/J/E66BIPQ06CupUhDA66iQ/q155.jpg)
155) Apenas questão de lógica.
Veja, vamos colocar alguns pontos coloridos na cadeira aberta:
Agora imagina esses pontos coloridos se unindo ao fechar a cadeira e pondo-a de lado.
Veja que a parte de cima formaria um retângulo, as parte em amarelo e laranja dariam a impressão de estarem unificadas, bem como as parte em verde, as partes em azul e roxo formariam um quadrado ao fechar esse ''x'':
A alternativa que mais se assemelha a esse desenho é a alternativa C.
Resposta C
/i.s3.glbimg.com/v1/AUTH_59edd422c0c84a879bd37670ae4f538a/internal_photos/bs/2016/Y/l/k6BAguRQAr9IlSvJCKKg/156.jpg)
156) Temos algumas informações dadas no enunciado.
Diz que para cada metro quadrado de área ocupada possuímos uma densidade de 4 pessoas.
O organizador do evento registra que às 10 horas da manhã um quadrado de lados de 500m tem sua área totalmente ocupada.
Ou seja, se para cada metro quadrado a densidade de pessoas é 4 e o quadrado tem 500 metros de lado, basta primeiro sabermos a área desse quadro, ou seja: l² -> 500² = 250000.
Em 25000 metros de área, quanto seria a densidade demográfica dessas pessoas?
250000 * 4 = 1000000
Às 10 da manhã já sabemos que temos 1000000 pessoas presentes no evento.
Depois é informado que à cada hora até o início do evento, a taxa de pessoas aumentará em 120000.
Sabemos que o evento se inicia às 4 horas da tarde (16 horas) e que às 11 horas da manhã já teríamos então mais 120.000 pessoas.
Para saber quantas pessoas teríamos ao todo no início do evento (às 16 horas) basta fazer uma regra de três.
Das 10 da manhã até às 16 horas se passaram 6 horas, ou seja:
Se na primeira hora do aumento de pessoas teremos 120.000 pessoas, quantas teríamos daqui 6 horas?
120.000 --- 1
x ------ 6
x = 120.000 * 6 = 720.000
Então desde às 10 horas até às 16 horas teríamos um total de 1.720.000 pessoas
720.000 do cálculo que acabamos de fazer e aquelas 1000000 que estavam às 10 horas ocupando o quadrado de 500 metros de lado.
É dito no problema que para cada 2000 pessoas se faz necessário um policial.
O problema quer saber, no início do evento quantos policiais serão necessários?
2000 pessoas ------ 1 policial
1.720.000 pessoas ------- y policiais
y = 1720000/2000
y = 860
Resposta E
/i.s3.glbimg.com/v1/AUTH_59edd422c0c84a879bd37670ae4f538a/internal_photos/bs/2016/A/m/Ylu7CLQvCZtovtus0h6w/157.jpg)
157) Outra questão relacionada à média, porém agora um pouco mais elaborada.
Para tirar a média de algo nós somamos todos os valores apresentados e dividimos pela quantidade de informações referentes a esse valor.
Aqui nós temos o caso de um dos valores ser desconhecido, ou seja, no caso, uma incógnita, que é justamente o que queremos encontrar.
Esse é o valor do lucro mínimo da empresa no mês de Junho.
Chamaremos então esse valor de x.
Se numa média nós somamos todos os valores apresentados então faremos o mesmo aqui:
21 + 35 + 21 + 30 + 38 + x
O 'x' ali no caso é o valor do lucro do mês de Junho que não sabemos de quanto que é.
Somando os termos conhecidos ficaremos com:
145 + x
E ainda para retirarmos a média de algo, devemos dividir pela quantidade de informações referentes.
Temos 5 meses apresentados na tabela (de Janeiro à Maio) e ainda como estamos incluindo 'x' na média, temos também que considerar o mês de Junho, ou seja, 6 meses:
145 + x /6
Agora preste atenção no enunciado: Ele nos diz que para o gerente permanecer na empresa, a média de lucros da mesma deva ser no mínimo de 30 mil reais.
Ou seja, nosso objetivo é 30 mil reais, em outras palavras, devemos criar uma equação que satisfaça os 30 mil reais, entende?
Logo, toda essa média que acabamos de fazer (145 + x/6) deva dar exatos 30 mil reais, ou seja:
145 + x/6 = 30
Agora resolvendo a equação, o 6 passa pro outro lado da igualdade multiplicando:
145 + x = 30*6
145 + x = 180
Isolando x:
x = 180 - 145
x = 35
Se x = 35, isso significa que o lucro do próximo mês (Junho) deve ser de no mínimo 35 mil reais, para no final das contas, a média de lucros da empresa ser equivalente a 30 mil reais, assim o gerente permanecerá na empresa.
Apenas conferindo:
21 + 35 + 21 + 30 + 38 + 35/6 = 30
Resposta E
/i.s3.glbimg.com/v1/AUTH_59edd422c0c84a879bd37670ae4f538a/internal_photos/bs/2016/z/C/upB7RPQxWIOaEfrdnRZQ/158.jpg)
158) Esse problema envolve uma função de primeiro grau, pois aqui encontramos um gráfico de uma reta.
A fórmula para uma função de primeiro grau é dada através de:
y = ax + b
Para y e x podemos adotar qualquer ponto que pertence à essa reta.
O ponto (1,30) é um deles, já que suas coordenadas se encontram claras no gráfico.
Temos então para x = 1 e y = 30, logo:
30 = a*1 + b ou
30 = a + b
Como não temos os valores dos coeficientes a e b, devemos estipular um sistema de primeiro grau para encontrar esses valores, ou seja, recorrer a outro ponto da reta.
(6,10) por exemplo, seria uma ótima escolha, pois é agora o único ponto que está descrito com clareza no gráfico.
Para x = 6 e y = 10, ou seja:
10 = a*6 + b ou
10 = 6a + b
Nosso sistema então fica como sendo:
30 = a + b
10 = 6a + b
Podemos isolar 'b' na primeira equação, veja:
30 = a + b
-b = -30 + a * (-1)
b = 30 - a
Substituindo 'b' na segunda equação, podemos encontrar o valor de 'a':
10 = 6a + b
10 = 6a + 30 - a
10 = 5a + 30
10 - 30 = 5a
-20 = 5a
-20/5 = a
-4 = a
Então temos que a = -4
Para encontrarmos o valor de 'b' basta substituir 'a' em qualquer uma das equações por -4:
30 = a + b
30 = -4 + b
30 + 4 = b
34 = b
Por fim, temos que nossa função (agora com os coeficientes 'a' e 'b' conhecidos) fica como sendo:
f(x) = -4x + 34
O que queremos encontrar é 'x', ou seja, no gráfico através da coordenada x, onde será o ponto da reta que irá resultar em 0% de capacidade, ou seja, quando o reservatório estiver esvaziado por completo.
A capacidade do reservatório está em função de y no gráfico, ou seja, a equação deve ficar:
y = -4x + 34
0 = -4x + 34
4x = 34
x = 34/4
x = 8,5
Ou seja, se prolongarmos o gráfico dessa reta, teríamos mais ou menos o seguinte:
Logo, após o sexto mês, o reservatório se encontraria vazio quase no nono mês, na metade do oitavo mês para ser mais exata.
Ou seja, se passariam 2 meses e meio para que isso acontecesse: 8,5 - 6 = 2,5
Resposta A
/i.s3.glbimg.com/v1/AUTH_59edd422c0c84a879bd37670ae4f538a/internal_photos/bs/2016/6/o/REJ7A7Tdmd9R6EA8sfiQ/159.jpg)
159) Outra questão de média.
Tirando a média de vacinas aplicadas, teremos:
21 + 22 + 25 + 31 + 21/5 = 24
O estoque dos próximos meses, como dito no problema, deve ser igual à média de vacinadas aplicadas vezes 12:
estoque = 24 * 12
estoque = 288
Alerta de pegadinha: Porém, esse seria o estoque se o mesmo estivesse vazio desde o primeiro mês.
Se marcar a alternativa E você estaria errando!
Lembre-se que no primeiro mês haviam 228 vacinas e o posto utilizou 120 vacinas (vide a quantidade de vacinas aplicadas).
Então dessas 228 vacinas, 120 foram usadas, ou seja, restaram 108 vacinas.
Então o estoque deve ser a quantidade total de vacinas que encontramos, menos a quantidade de vacinas que já temos:
288 - 108 = 180
Resposta B
/i.s3.glbimg.com/v1/AUTH_59edd422c0c84a879bd37670ae4f538a/internal_photos/bs/2016/b/4/tzOziXR3uucJBM2AkPaQ/160.jpg)
160) Essa questão de logaritmos pode ser difícil se você não conhecer a lei do resfriamento de Newton, cuja a fórmula se dá por:
T seria a temperatura final
Ta seria a temperatura ambiente
T0 seria a temperatura inicial
'e' seria a constante de resfriamento
kt seria o tempo de resfriamento.
Como não foi dado no problema a temperatura ambiente, podemos descartar Ta na equação, ficaremos com:
Veja que a temperatura final da liga é de 30 ºC, bem como a temperatura inicial é de 3000 ºC.
Substituindo esses valores na fórmula teremos o seguinte:
A constante de resfriamento é aquele 1% que a liga metálica resfria à cada meia hora.
Se à cada meia hora é resfriado 1% de um todo (que costuma ser 100%) isso significa que teremos 99% do todo na primeira meia hora:
Dizer que algo está à 99% é o mesmo que dizer 99/100. Trabalharemos com decimais para facilitar o cálculo:
Como à cada meia hora o metal resfria 1%, podemos dizer que temos 2 tempos de meia hora para dar uma hora ao todo. (Já que o enunciado pede o tempo em hora, não em minuto).
Então:
Você pode passar o 3000 que está multiplicando 99/100 pro outro lado da igualdade, dividindo:
Simplificando 30 e 3000 você ficará com:
E ainda simplificando 3/300 por 3, teremos:
Já que temos uma incógnita no expoente de uma potência, podemos aplicar logaritmo dos dois lados da igualdade:
Agora que temos log de ambos lados da equação podemos utilizar as propriedades operatórias dos logaritmos para resolver essa equação.
A primeira propriedade nos diz que se tivermos logaritmos de mesma base dividindo, podemos subtraí-los, então:
Nesse momento podemos resolver os logaritmos:
Log de 1 = 0
Log de 100 = 2
Log de 99 teremos:
99 | 3
33 | 3
11 | 11
1
Ou seja:
Log99 = Log3² * Log11
Outra propriedade dos logaritmos nos diz que se ambos logs tiverem mesma base e estiverem multiplicando, podemos somá-los:
log99 = log3² + log11
Então teremos por fim:
-2 = log3² + log11 - 2²t
Outra propriedade nos diz que o expoente de um log pode multiplicar seu logaritmando:
-2 = 2t(2*log3 + log 11 - 2)
O enunciado nos diz que log 3 = 0,477 e log 11 = 1,041 então temos que:
-2 = 2t(2*0,477 + 1,041 - 2)
Resolvendo:
-2 = 2t * -0,005
-2 = -0,01t
200 = t
Então essa liga metálica que está à 3000 ºC e que à cada 30 minutos resfria 1%, vai chegar à 30 graus célsius em 200 horas.
Resposta D