Os Logaritmos: Propriedades Operatórias ~ Aulas da May

Na aula passada você conheceu os logaritmos, aprendeu como resolver pequenas equações logarítmicas, descobriu como utilizar a tábua de logaritmos e conheceu os logaritmos decimais. Nesta aula, iremos avançar mais um pouco e iremos conhecer as Propriedades Operatórias dos Logaritmos, vamos lá?

Propriedade 1: Logaritmo de um produto:
Se temos uma multiplicação de logaritmos com bases iguais, então temos consequentemente uma soma entre eles:

$\log_{a}(b*c) = \log_{a} b + \log_{a} c$

Propriedade 2: Logaritmo de um quociente:
Se temos uma divisão entre logaritmos de bases iguais, então temos consequentemente uma subtração entre eles:

$\log_{a}(\frac{b}{c}) = \log_{a} b - \log_{a} c$

Propriedade 3: Logaritmo de uma potência:
Se temos uma potência de logaritmo, então o expoente dessa potência passa a ser um número que multiplicará o logaritmo de sua base:

$\log_{a}{b}^{n} = n*\log_{a}b$

Bem, essas são as principais propriedades operatórias dos logaritmos, ainda falta mencionar a quarta propriedade sobre mudança de base, mas isso deixaremos exclusivamente para a próxima aula.
Pois bem, guarde essas propriedades pois usaremos muito delas nas aulas posteriores e nesta aula também!
Mas, você deve ter visto esse monte de letras misturadas e não deve ter compreendido muito bem, certo? Não se preocupe, nós vamos aprender passo à passo, como utilizar corretamente cada uma dessas propriedades, vamos ver diretamente um exemplo prático para essas aplicações?

Sabendo que log 2 = 0,3 e log 3 = 0,47; determine log 24:

$\log 24$

Se temos aqui uma base oculta, então temos consequentemente uma logaritmo decimal, correto? Então não tem segredo, basta fatorar o 24:

24 | 2
12 | 2
6 | 2
3 | 3
1

Então temos 2³.3, certo? Logo temos:

$\log 2³ . \log 3$

Bom, aqui podemos aplicar duas propriedades das operações entre logaritmos, primeiramente a propriedade 1, que diz que quando temos uma multiplicação entre logaritmos de mesma base, temos consequentemente uma soma entre eles, então:

$\log 2³ + \log 3$

Agora perceba que podemos aplicar mais uma propriedade operatória entre logaritmos, a propriedade 3 que nos diz que quando temos uma potência de logaritmo, devemos passar esse expoente da potência para frente do log, multiplicando o logaritmo de sua base, então:

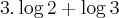
$3.\log 2 + \log 3$

Perceba que o expoente 3 do log de 2, agora multiplica o mesmo.
Pois bem, segundo o enunciado do problema: Log2 = 0,3 e Log3 = 0,47
Substituindo então log de 2 e log de 3 por esses números, teremos:

3.0,3 + 0,47

Multiplicando 3 por 0,3 iremos obter 0,9:

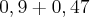
0,9 + 0,47

Ué, agora não há dificuldades, basta somar 0,9 com 0,47 para obter o resultado final:

0,9 + 0,47 = 1,37

Então o log de 24 é igual à aproximadamente 1,37:

log24 = 1,37

Outros exemplos:

Vamos calcular os logs dos seguintes números:

$log18\par log125 = \par log600 = \par log100000 = \par log{4}^{5} =\par log{24}^{9} =\par log320 =\par log ({6}^{5})^{3} = \par log0,44 = \par log1,25 = \par log \sqrt[6]{{12}^{3}} =\par log \sqrt[]{128} = \par log \sqrt[7]{132} = \par log \sqrt[]{2,6} =\par$

$log \frac{42}{3} = \par$ $log \frac{4}{5} =$

Então iremos calcular um por um, para que você possa pegar o jeito!

Antes disso, tenha em mente que é sempre bom decorar os logs de alguns números primos como: log2, log3, log5, log7, log11 e log13, que serão muito utilizados aqui:

log2 = 0,3
log3 = 0,5
log5 = 0,7
log7 = 0,85
log11 = 1,04
log13 = 1,11

Claro, esses não são os logaritmos exatos desses números, mas são bem aproximados e não alteram muito a resolução.

Primeiro log a ser calculado:

log18

O primeiro passo a se fazer é decompor em fatores primos o número 18:

18| 2
9 | 3
3 | 3
1

Então temos:

2.3²

log2 * log3²

Aplicando a propriedade dos produtos dos logaritmos, iremos transformar essa multiplicação em soma:

log2 + log3²

Agora temos que aplicar a terceira propriedade, a propriedade da potência do logaritmo:

log2 + 2.log3

Por fim, já sabemos que log de 2 = 0,3 e log de 3 = 0,5; então:

0,3 + (2*0,5 )
0,3 + 1 = 1,03

Então o log de 18 é igual à aproximadamente 1,3.

Próximo:

log125:

Decompondo o 125 em fatores primos:

125| 5
25 | 5
5 | 5
1

5³

Então temos: log5³
Para resolver esse logaritmo, basta aplicar a propriedade 3, da potência de logaritmos:

3*log5
3*0,7 = 2,1

Então o log de 125 é igual à aproximadamente 2,1.
Confira esse resultado em sua calculadora cientifica, onde ao digitar 125 e depois pressionar a tecla ''log'' aparecerá o resultado: 2,096... Ou seja, um resultado bem aproximado à 2,1; o que encontramos.
Continuando...

log600

A gente bem que poderia decompor esse 600 em fatores primos, mas você não acha que há um modo mais fácil de resolver esse logaritmo?
Veja bem, 600 é a mesma coisa que: 6*100, não?
Então podemos fazer o log de 600 da seguinte forma:

log6 * log100

Aplicando a primeira propriedade dos logaritmos:

log6 + log100

Sabemos também que log100 = 2 (só contar a quantidade de zeros); então:

log6 + 2

Agora sim podemos decompor o 6 em fatores primos, o que é muito mais fácil que decompor o 600:

6 | 2
3 | 3
1

Então teremos:

log2 * log3 + 2
log2 + log3 + 2
0,3 + 0,5 + 2 = 2,8

Próximo...

log100.000

Antes de entrar em pânico graças ao tamanho do número, pense... É só contar a quantidade de zeros: log100.000 = 5

Mais um...

$log{4}^{5}$

Aqui é fácil, basta aplicar a propriedade da potência de logaritmos, primeiramente:

5*log4

log4 = 2² (Decompondo em fatores primos); logo:

5*log2²

Novamente aplicando a mesma propriedade das potências de logaritmos:

5*2*log2
10*0,3 = 3

Vamos ao próximo:

$log{24}^{9}$

Começamos aplicando a 3ª propriedade dos logaritmos:

9*log24

Decompondo o 24:

24|2
12|2
6 | 2
3 | 3
1

2³ * 3 = log2³ * log3

Aplicando novamente essa propriedade de potências, teremos:

3*log2 * log3
3*0,3 + 0,5
0,9 + 0,5 = 1,4

Então...

9*1,4 = 12,6

Próximo a ser resolvido:

log320

320 é a mesma coisa que: 32*10, então:

log32 * log10

Aplicando a primeira propriedade:

log32 + log10

Sabendo-se que log10 =1, temos:

log32 + 1

Decompondo o 32:

32|2
16|2
8 |2
4 |2
2 |2
1

${2}^{5}$

Então temos:

$log{2}^{5} + 1$

Aplique a terceira propriedade:

$5*log{2} + 1\par 5 * 0,3 + 1\par 1,5 + 1 = 2,5$

Próximo a ser resolvido:

$log({6}^{5})^{3}$

Pela propriedade das potências, podemos multiplicar os expoentes e conservar a base, logo:

$log({6}^{5})^{3} \rightarrow log{6}^{5*3} \rightarrow log{6}^{15}$

Então ficamos com:

$log{6}^{15}$

Aplique a 3ª propriedade:

15*log6

Ao fatorar o 6 você irá encontrar: log2 * log3, então aplique a primeira propriedade: log2 + log3
Sabendo os logs de 2 e 3, obtenha: 0,3 + 0,5 = 0,8; então:

15*0,8 = 12

Vamos ao próximo...

log0,44

Aqui finalmente iremos utilizar a segunda propriedade, do quociente de um logaritmo:

Perceba que podemos transformar esse decimal numa simples fração:

$log\frac{44}{100}$

Agora que temos uma divisão de logaritmos, podemos utilizar a segunda propriedade: Ou seja, se temos uma divisão de logaritmos, temos consequentemente uma subtração entre eles:

$log\frac{44}{100} = log44 - log100$

Sabemos que log100 = 2, então basta fatorar o 44:

44|2
22|2
11|11
1

Então temos:

log2² * log11

Aplicando as propriedades da potência e do produto:

2*log2 + log11

2 * 0,3 + 1,04 = 2,1

Então por fim temos:

1,64 - 2 = -0,36

Lembre-se: Sempre que um número for menor que 1, seu logaritmo será negativo, é o caso do log de 0,44.

Mais outro:

log1,25

Novamente podemos transformar esse log de número decimal, numa fração:

$log\frac{125}{100}$

Aplicando a segunda propriedade teremos:

log125 - log100

Sabendo que: log100 = 2:

125 - 2

Agora fatoremos o 125:

125|5
25 |5
5 | 5
1

log5³ - 2

3*log5 - 2

3*0,7 -2 = 0,1

Agora vamos resolver:

$log\,\sqrt[6]{{12}^{3}}$

Aqui o segredo é nos livramos da raiz! Como podemos fazer isso? Simples! Iremos radiciar transformando essa raiz, num número com expoente fracionário!
Então teremos:

$log {12}^{\frac{3}{6}} \rightarrow log {12}^{\frac{1}{2}}$

Note que simplifiquei 3/6 por 3 e fiquei com 1/2.
Agora podemos aplicar a terceira propriedade dos logaritmos que envolve as potências:

$\frac{1}{2} * log12$

Vamos encontrar o log de 12 para terminarmos essa multiplicação. Para isso, fatore o 12:

12|2
6 |2
3 |3
1

log2² * log3
2*log2 + log3
2*0,3 + 0,5 = 1,1

Então temos:

$\frac{1}{2} * 1,1$

Agora faça a multiplicação como se pede! Você tem duas possibilidades de fazer isso:

1ª Possibilidade: Você pode transformar o meio em decimal:

$\frac{1}{2} = 0,5$

Agora basta multiplicar:

0,5 * 1,1 = 0,55

2º Possibilidade: Ou pode multiplicar direto da forma como os números estão:

$\frac{1}{2} * \frac{1,1}{1} = \frac{1,1}{2} = 0,55$

Ai está!

Podemos resolver agora:

$log\,\sqrt[]{128}$

Novamente devemos nos livrar desta raiz, como a raiz quadrada de 128 não é exata, teremos que decompor o 128:

128|2
64 |2
32 |2
16 |2
8 |2
4 |2
2 |2
1

Teremos então:

$log\,\sqrt[]{{2}^{7}}$

Mas ainda não nos livramos da raiz! Para isso vamos ter que radiciar:

$log\,\sqrt[]{{2}^{7}} = log{2}^{\frac{7}{2}}$

Agora sim! Vamos aplicar a 3ª Propriedade:

$\frac{7}{2} * log2$

Sabemos que o log de 2 é 0,3; então:

$\frac{7}{2} * 0,3$

Vamos resolver essa multiplicação diretamente com o número fracionário, mas se você preferir, você pode transformá-lo num número decimal, o resultado obtido será o mesmo em ambos os casos, como você pode perceber no exemplo anterior.

$\frac{7}{2} * \frac{0,3}{1} = \frac{2,1}{2} = 1,05$

Vamos resolver mais um?

$log\,\sqrt[7]{132}$

Radiciando:

$log\,\sqrt[7]{132} = {132}^{\frac{1}{7}}$

Aplicando a propriedade 3:

$\frac{1}{7} * log132$

Resolvemos o log de 132 decompondo o mesmo:

132|2
66 |2
33 |3
11 |11
1

log2² * log3 * log11
2*log2 + log3 + log11
2*0,3 + 0,5 + 1,04 = 2,14

Então substituindo log132 por 2,14 a gente vai ter:

$\frac{1}{7} * 2,14$

Agora multiplique direto ou transforme o 1/7 em decimal:

$\frac{1}{7} * \frac{2,14}{1} = \frac{2,14}{7} = 0,30$

Gostou? Vamos fazer mais uma então!

$log\,\sqrt[]{2,6}$

Não se aflija... Podemos transformar esse 2,6 numa fração!

2,6 é o mesmo que: $\frac{26}{10}$

Então temos:

$log\,\sqrt[]{\frac{26}{10}}$

Vamos eliminar essa raiz, radiciando-a. Poderíamos aplicar a propriedade das raízes sobre divisão entre elas, mas veja que com os logaritmos podemos encurtar o processo:

Elimine a raiz, transformando-a num número com expoente fracionário:

$log\,\sqrt[]{\frac{26}{10}} =\, log{\frac{26}{10}}^{\frac{1}{2}}$

Agora aplique a 3ª propriedade:

$\frac{1}{2} * log\frac{26}{10}$

Feito isso, temos uma divisão entre logaritmos! O que isso te lembra? Exatamente! A propriedade 2, então:

log26 - log10

Já sabemos que log10 = 1 -> log26 - 1
Então basta encontrarmos o log de 26 fatorando-o!

26|2
13 |13
1

log2 * log13
0,3 + 1,11 = 1,4

Então temos:

1,4 - 1 = 0,4

Agora substitua log26/10 por 0,4:

$\frac{1}{2} * 0,4$

A metade de 0,4 é igual à 0,2
E está aí o resultado!

Agora vamos resolver rapidamente os logs fracionários (Você viu vários exemplos acima de como resolvê-los!)

Primeiro a ser resolvido:

$log \frac{42}{3} = \par$

Vemos que temos uma divisão entre logaritmos, então temos uma subtração entre eles:

log42 - log3

Fatore o 42:

42|2
21|3
7 |7
1

log2 * log3 * log7
log2 + log3 + log7
0,3 + 0,5 + 0,85 = 1,65

1,65 - log3
1,65 - 0,5 = 1,15

Próximo:

$log \frac{4}{5} =$

Aplique a segunda propriedade:

log4 - log5
log2² - log5
2*log2 - log5
2*0,3 - 0,7 = -0,1

Logaritmos com base diferentes dez:
Vamos ver também como realizar essas operações com logs de bases diferentes de 10, por exemplo:

$\log_2({4*8}) = x$

Uma multiplicação entre logaritmos pode se tornar uma soma, contanto que ambos continuem com a mesma base, então:

$\log_24 + \log_28 = x$

Agora basta encontramos os logs de 4 na base 2 e 8 na base 2, veja:

$2^x = 4$

Sabemos que o número 2 é o número que elevado à dois nos resulta em quatro, então
$2^x = 2^2$

O próximo log também é fácil, fácil:

$2^x = 8$

Se você já está craque neste tipo de equação, nem precisaremos fatorar o 8, pois você já deve saber que:

$2^x = 2^3$

Então temos que o log de 4 na base 2 é 2 e o log de 8 na base 2 é 3, portanto temos:

2 + 3 = x
5 = x

Por tanto, sabendo que x vale 5, para conferir a pequena equação podemos dizer o seguinte, através da definição de logaritmos:

$log_2(4*8) = 5 \Leftrightarrow 2^5 = 4*8$

Pois 2 é a base, 5 (que é o expoente da potência) era o logaritmo, e 4*8 é o logaritmando.
2 elevado à 5 é 32 e 4*8 é 32, então

32 = 32
Equação satisfeita!

Você poderá ver mais exemplos sobre esse tipo de equação nas aulas posteriores sobre equações com logaritmos!

E está feito!
Espero que depois de todos esses exercícios resolvidos você tenha pegado o jeito com as operações em logaritmos!
Leia a próxima aula para continuar com o assunto e bons estudos!!

15 comentários:

Unknown9 de agosto de 2016 às 11:03
Parabens May, uma moça muito inteligente, apesar de não ter comentarios em seu blog, pode ter certeza que seu raciocinio ja ajudou muitas pessoas.
ResponderExcluir
Respostas
Unknown18 de setembro de 2016 às 05:55
muito obrigado. vi essa materia a muito tempo e precisava de lembrar de alguns conceitos. valeu mesmo!!
ResponderExcluir
Respostas
Unknown29 de outubro de 2016 às 04:51
May peco ajuda
como como resolver uma diferenca de logaritimos de bases diferentes como por exemplo:
log de 32 na base 2, menos log de 1/27 na base 3, menos log de raiz quadrada de 32 na base 32
ResponderExcluir
Respostas
Unknown29 de outubro de 2016 às 04:52
May peco ajuda
como como resolver uma diferenca de logaritimos de bases diferentes como por exemplo:
log de 32 na base 2, menos log de 1/27 na base 3, menos log de raiz quadrada de 32 na base 32
ResponderExcluir
Respostas
Unknown2 de maio de 2017 às 20:02
como resolver a solução logarítmica:
2log2(x+1)-log4(x²+7)=-1
ResponderExcluir
Respostas
AyeshaZZ14 de outubro de 2017 às 16:21
May como faço pra resolver uma fração onde a base e o logaritimando são frações como oor exemplo;
Log 625/16
4/5
ResponderExcluir
Respostas
5433 de janeiro de 2018 às 03:14
Muchas gracias por el excelente material didáctico. Me topé con este sitio, y me gustó mucho. Saludos
ResponderExcluir
Respostas
Unknown10 de maio de 2018 às 21:27
Parabéns, tem uma propriedade rara nos livros e você postou e que me ajudou bastante, obrigada
ResponderExcluir
Respostas
Unknown26 de novembro de 2018 às 08:27
como resolvo isso: 15^x + 9^x = 25
ResponderExcluir
Respostas

Adicionar comentário

Aulas da May

quarta-feira, 4 de junho de 2014

Os Logaritmos: Propriedades Operatórias

15 comentários:

Entre em contato: