Bem pessoal, não tem como encurtar o título dessa postagem, pois é isso mesmo que você leu! Aprenda de uma forma simples e rápida, como obter qualquer termo de uma P.A dada, sabendo-se apenas dois termos, tudo isso, com apenas uma fórmula! Quer ver?
Dada uma Progressão Aritmética, cujo termo a10 = 33 e a17 = 68, determine o termo a32.
Bem, não podemos aplicar a fórmula do termo geral da P.A, pois não conhecemos a razão, o número de termos, muito menos o a1, por isso devemos recorrer à outra fórmula que eu aprimorei da original, a fórmula é a seguinte:

Não se assuste, a fórmula é fácil de ser usada:
t1 --> Primeiro termo dado no problema;
t2 --> Segundo termo dado no problema;
at1 --> É o número do primeiro termo, assim como ''at2'' é o número do segundo termo;
r --> Razão da P.A
Então no nosso caso, o primeiro termo dado é 33 (a10); o segundo termo dado é 68 (a17) e os números dos termos são, respectivamente 10 e 17, certo? Então aplique esses valores na fórmula e teremos:

Resolva a equação:



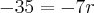
Como não nos interessa um resultado negativo, multiplique tudo por -1 e troque os sinais:


Aqui está a razão da nossa P.A! E com ela podemos encontrar qualquer termo da mesma, sabendo-se pelo menos um dos termos.
No caso, nós queremos encontrar o termo a32, e sabemos os termos: a10 e a17, agora vai de sua escolha utilizar qualquer um dos termos conhecidos, eu vou usar o a10, mas com a17 dá no mesmo!
Vamos aplicar a fórmula novamente, mas agora em função ao a32 e sabendo a razão da P.A:
t1 = 33;
t2 = x (o que queremos achar);
at1 = 10;
at2 = 32
r = 5 (encontramos anteriormente)
Aplicação na fórmula:


Ou seja, o trigésimo segundo termo (a32) desta P.A é igual à 143.
Uma obversão sobre esta fórmula: ''t1'' sempre deve ser o menor termo fornecido, assim como ''t2'' deverá ser o maior termo fornecido.
Outro exemplo?
Na P.A à seguir, onde a67 = 1321 e a75 = 1353, calcule o termo a89.
Vamos primeiro encontrar a razão da P.A, em função aos dois termos fornecidos:
t1 = 1321;
t2 = 1353
at1 = 67
at2 = 75
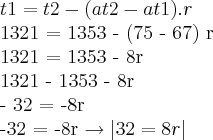


Então a razão é 4! Basta agora reutilizar a fórmula, mas agora em função ao termo a89, e utilizando qualquer termo conhecido para t1, no caso, vou usar a67, mas com a75 também dará certo!
t1 = 1321
t2 = x
at1 = 67
at2 = 89
r = 4

Então o termo a89 da P.A é igual à 1409.
E é isso...Espero que tenham gostado da dica, até mais!
quinta-feira, 5 de junho de 2014
Arquivo de ajuda: Encontrar o termo de qualquer P.A à partir de dois termos
21:55
1 comment
Assinar:
Postar comentários (Atom)




obrigado may S2 ajudou muitooo
ResponderExcluir