Matrizes: Conceitos básicos e tipos de Matrizes

O que é?
Em matemática, a Matriz é representada por uma tabela contendo elementos numéricos, onde a mesma pode possuir ''m'' linhas e ''n'' colunas!
As matrizes são essenciais para o estudo de determinantes e sistemas lineares.
Vamos ver como representar uma matriz:

Veja a matriz ''A'' abaixo:



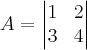
Uma matriz, como já explicado, é composta por elementos numéricos de ''m'' linhas e ''n'' colunas, onde na horizontal temos as colunas, e na vertical temos as linhas:

Note que na representação acima, a seta vermelha corresponde a quantidade de colunas, e a seta azul corresponde a quantidade de linhas.
Ainda nesse exemplo, perceba que temos a mesma quantidade de colunas, que são duas, e a mesma quantidade de linhas, ou seja, também duas.
Sendo assim, chamamos essa Matriz de Matriz quadrada 2x2. (Lê-se ''dois por dois'')
Ela é quadrada por ter a mesma quantidade de linhas e colunas, e ''2x2'' por ter duas linhas e duas colunas.
Veja esta outra matriz quadrada:




Essa matriz quadrada tem ordem 3x3 (Lê-se ''três por três''), por possuir 3 linhas e 3 colunas.
No caso dessa matriz quadrada de ordem 3x3 o mais correto seria dizer também: ''Matriz quadrada de ordem 3'', pois fica subentendido que ela possui 3 linhas e 3 colunas pelo fato dela ser quadrada.

Mas como se chamam matrizes com ordens diferentes?

Por exemplo, essa aqui:



Essa matriz chama-se ''Matriz retangular'', por possuir o número de linhas diferente do número de colunas.
Essa matriz tem ordem 3x2 (Lê-se ''três por dois''), por possuir três linhas e duas colunas.
Sempre quando você for se referir à ordem da Matriz, o número de linhas vem primeiro que o número de colunas, sempre!

Pois bem, agora que você conheceu alguns elementos básicos das matrizes, vamos ver como os elementos dentro delas são organizados?

Organização da Matriz:

Veja esta matriz:



Nessa matriz quadrada de ordem 2, temos 4 elementos inseridos na mesma, elementos esses que estão organizados da seguinte forma: 

Na primeira linha e primeira coluna, temos o elemento a1.1! Mas o que isso significa? Significa exatamente isso, os números após o elemento da matriz, são correspondentes de acordo com sua posição na mesma.
Temos por exemplo, o elemento a1.2. O que isso quer dizer? Que o elemento está na primeira linha e segunda coluna.
E o elemento a2.1? O elemento a2.1 está inserido na segunda linha e primeira coluna desta matriz, assim como o elemento a2.2 está inserido na segunda linha e segunda coluna da matriz.
Vá se acostumando com essa ideia, e tenha sempre em mente que o número que vem à frente da posição do elemento na matriz, é correspondente à linha, e o número em seguida da correspondência à linha da matriz, é corresponde à coluna da mesma, assim como é feito para determinar a ordem da matriz.

Agora me responda algumas coisas referentes à essa matriz (responda para si mesmo):



1) Quantos elementos temos nessa matriz?
2) Qual é a ordem desta matriz?
3) Que tipo de matriz ela é?
4) O elemento ''6'' está em qual posição na matriz?
5) E o elemento ''4'?

Bom vamos lá...

• Temos 12 elementos nesta matriz, basta notar que ela foi disposta em uma ordem crescente de um à doze;
• A ordem desta matriz é 3x4 (Lê-se ''três por quatro'') por conter três linhas e quatro colunas;
• Esta matriz é do tipo retangular, por conter o número diferente de linhas e colunas;
• O elemento ''6'' está na posição: a2.2, por estar na segunda linha e segunda coluna;
• O elemento ''4'' está na posição: a1.4 por estar na primeira linha e quarta coluna.

Em problemas envolvendo as matrizes, não costumamos chamar as linhas de linhas e as colunas de colunas, nós estamos acostumados a representar as linhas por ''i'' e as colunas por ''j''.

Veja este exemplo para entender melhor:

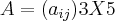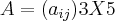Na Matriz  encontre os elementos que serão solicitados:

a3.2 =

a1.1 =

a3.4 =

a2.5 =

Como assim ''Matriz A = (aij) 3x5''?

Isso significa que a Matriz retangular ''A'', possui os elementos dispostos em i=3 e j=5, ou seja, três linhas e 5 colunas.

Bem, agora que sabe disso... Tente resolver o que se pede, ou seja, encontrar os elementos pedidos no problema, dentro desta matriz ''A''.

Vamos lá...

A3.2 => O elemento que está nesta posição, deve estar na terceira linha e segunda coluna. Quem é? Procure por lá...

O número 8 está nesta posição, não? Note que ele está na terceira linha e na segunda coluna da mesma.

a1.1 => O elemento deve estar na primeira linha e primeira coluna! Quem é? O número 3, certo?

a3.4 => O elemento que se encontra na terceira linha e quarta coluna é o  ''x''.

a2.5 => Por fim, o elemento que está na segunda linha e quinta coluna, é o numero 0. Então nesta matriz:

a3.2 = 8

a1.1 = 3

a3.4 = x

a2.5 = 0

Para ficar mais claro, agora vamos resolver um exercício bem básico referente à matrizes e seus elementos:

Numa matriz  encontre seus elementos sendo que: aij = 2i + 5j.

Bem, então temos uma matriz retangular de ordem 2x4, ou seja, duas linhas e quatro colunas.
Vamos construir nossa matriz nessa ordem, da mesma forma como fizemos nos exemplos acima:

2x4

Aí está nossa matriz organizada como se deve, na ordem 2x4.
Continuando... Lembrando sempre que ''i'' se refere às linhas da matriz e ''j'' às colunas, concluímos que:

Em nosso problema temos: 2i ou seja, 2*i. Sabendo disso, posso dizer que o número 2 está multiplicando o valor das linhas da matriz. O mesmo ocorre com 5j (5*j) em que o 5 que está multiplicando todas as colunas da matriz.
Vamos ver como fica?

Na primeira coluna e na primeira linha temos: a1.1
Então iremos multiplicar por dois a linha (que é 1) e por 5 a coluna (que também é 1):

1*2 + 5*1

Resolvendo...

2 + 5 = 7

Então nosso primeiro elemento na matriz "A" é igual à 7! Nossa matriz fica assim:

2x4

Por fim, o mesmo ocorrerá com todos os outros elementos na matriz, veja:

Temos agora o segundo elemento da primeira linha: a1.2
Resolvendo a matriz temos:

1*2 + 5*2
2 + 10 = 12

Nosso segundo elemento da primeira linha é o 12:

2x4

Vamos fazer agora os cálculos dentro da matriz para não nos perdemos?

2x4

Então resolvendo tudo ficamos por fim com:

 2x4


Perceba uma coisa muito interessante na matriz acima:

Na primeira linha temos: 7, 12, 17 e 22.
Note que ela cresce de 5 em 5.
O mesmo ocorre com a segunda linha: 9, 14, 19 e 24.

E note também que o elemento de a1.1 é 2 unidades menor que o elemento de a2.1:

a1.1 = 7
a2.1 = 9

7 + 2 = 9

O mesmo ocorre nos próximos elementos em suas respectivas linhas paralelas:
a1.2 = 12
a2.2 = 14

12 + 2 = 14

a1.3 = 17
a2.3 = 19

a1.4 = 22
a2.4 = 24

Note que os números ''5'' e ''2'' aparecem nessas coincidências.
5 é o número que cresce em cada elemento das colunas, e 2 é a diferença de unidades entre os elementos de cada coluna para sua respectiva linha.
E onde mais estão esses dois números aparecem? No próprio enunciado do problema, veja:

Numa matriz  encontre seus elementos sendo que: aij = 2i + 5j.

Agora você percebe que não havia necessidade de realizar tantos cálculos, não?

Bem, agora vamos falar de outra propriedade das matrizes:

As Diagonais:

Uma matriz possui duas diagonais: A ''diagonal principal'', que desce da esquerda pra direita, por exemplo:
Nessa matriz quadrada de ordem 3:



A diagonal principal está aqui: 

Temos ainda outro tipo de diagonal chamada de ''diagonal secundária'', que sobe da direita pra esquerda:

E a mesma matriz marcada com ambas diagonais:

Tipos de Matrizes:

Veremos agora alguns tipos de matrizes:

Matriz nula:
A matriz nula é aquela matriz em que todos os seus elementos são iguais à zero:


Matriz Linha:
Na matriz linha temos apenas uma linha na mesma:


Matriz Coluna:
E ao contrário da matriz linha, onde só temos uma linha da matriz, na matriz coluna, temos apenas uma coluna na mesma:


Matriz Oposta:
A matriz oposta é o inverso da matriz original, ou seja, basta você copiar a matriz original e para transformá-la em sua matriz oposta, basta trocar o sinal de todos os seus elementos, exemplo:





Sua matriz oposta é:



Matriz Identidade:
A matriz identidade é um tipo de matriz muito interessante, pois neste tipo de matriz todos os elementos na mesma devem ser zero, exceto na diagonal principal, onde os números devem ser todos 1:



Matriz Diagonal:
Na matriz diagonal todos os elementos devem ser zero também, mas diferente da matriz identidade, nesse tipo de matriz poderá existir qualquer elemento diferente de 1 na diagonal principal:





Matriz Transposta: 
Na matriz transposta você simplesmente troca os elementos das linhas para as colunas, e os elementos das colunas para as linhas, por exemplo:

2x3



Aqui a transposta de G, ou seja, matematicamente falando:  (G elevado à t = matriz transposta de ''G'')
Será:

3x2

Ou seja, antes a ordem era 2x3 e agora na matriz transposta passou a ser 3x2 e os elementos que compunham as linhas passaram a compor as colunas, assim como os elementos que compunham as colunas passaram a compor as linhas.
Para você poder visualizar melhor essa ''transformação'' veja a matriz original, e depois veja a sua matriz transposta abaixo:

Notou que os elementos da primeira linha passaram a compor a primeira coluna e os elementos da segunda linha passaram a compor a segunda coluna?
Pois então, é isso que você deve fazer para encontrar a transposta de uma matriz, simplesmente inverter as suas linhas e suas colunas.

Pois bem, a aula de definição de matrizes se encerra aqui! Porém, para continuar estudando o assunto clique aqui(link em breve) para completar este assunto referente às matrizes.
Bons estudos.