Trigonometria do Triângulo Retângulo

O que é Trigonometria?
A trigonometria é uma área da matemática onde estuda-se as relações entre triângulos retângulos e o comprimento de seus lados, sob diferentes valores de seus ângulos agudos. Em resumo, a trigonometria estuda os triângulos retângulos, mas não só apenas isso, a trigonometria também aborda outros assuntos na geometria, como esferas trigonométricas e outros triângulos, por exemplo. 
Mas para antes tentar compreender o estudo mais avançado sobre trigonometria, devemos estudar o básico, neste caso o básico a ser estudado seria o estudo do triângulo retângulo.
Mas o que é um triângulo retângulo?

A Definição de um Triângulo Retângulo:
Um triângulo retângulo na geometria é um triângulo que tem como principal característica, a presença de um ângulo reto (90 graus)  internamente, veja neste exemplo:


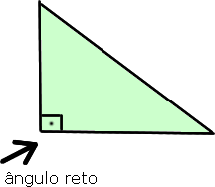
Perceba então que a principal característica de um triângulo retângulo é sempre a presença do ângulo reto de noventa graus, em um de seus cantos. Sem isso, um triângulo não pode ser dito como um triângulo retângulo.
Porém o ângulo reto não é o único elemento que forma o triângulo retângulo, veja abaixo:


Os Elementos de um Triângulo Retângulo:
Além do ângulo reto de 90°, um triângulo retângulo ainda possui outros elementos, como os catetos que formam seus cantos (para memorizar este nome, basta lembrar de ''cantetos'', pois eles definem os cantos do triângulo retângulo) , a hipotenusa e a presença de mais dois ângulos agudos internos (Ou seja, que são menores que 90°), mais conhecidos como ângulo alfa (α) e ângulo beta (β).
 Veja um exemplo da representação de um triângulo retângulo contendo seus elementos:




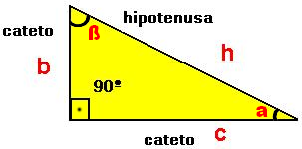
Esclarecendo a imagem acima: Temos o primeiro elemento do triângulo retângulo, o ângulo reto de 90°, e mais dois ângulos agudos internos, chamados de alfa (α) e beta (β).
Dois catetos representados pelas letras B e C e a hipotenusa representada pela letra H.
Normalmente nós descobrimos quem é a Hipotenusa e que são os Catetos, apenas observando a figura de um triângulo retângulo, e suas relações entre seus ângulos:
Relacionando o ângulo reto com a hipotenusa, podemos encontrá-la facilmente se sabermos que: A Hipotenusa sempre estará oposta ao ângulo reto, veja:




Sabemos também que a hipotenusa sempre será o lado maior do triângulo retângulo!
Para descobrir quem são os catetos, basta observar que são eles os responsáveis por formarem os cantos do triângulo retângulo:

Os segmentos em vermelho e azul na imagem acima, representam os catetos deste triângulo retângulo.
Porém, é meio incomodo não sabermos de qual cateto estamos nos referindo, já que temos dois! Por isso, eles foram nomeados de Cateto Oposto e Cateto Adjacente.
O Cateto adjacente sempre será aquele que está próximo ao ângulo agudo referido, já o Cateto oposto será aquele que estará sempre ao oposto do ângulo agudo referido.
Como temos dois ângulos agudos, alfa e beta, as nomenclaturas dos catetos são diferentes para cada um, dependendo de sua posição no triângulo retângulo.
Por exemplo, para o ângulo alfa desta figura, temos que:

Onde o Cateto adjacente (em azul) está próximo ao ângulo alfa, e o Cateto oposto (em vermelho) está oposto à este ângulo.
Mas no caso do ângulo beta as coisas mudam! Os nomes dos catetos serão diferentes, pois o que é adjacente para alfa é oposto para beta, e vice-versa, veja:

Perceba que agora o Cateto adjacente(em azul) à beta, forma a altura do triângulo retângulo, e o Cateto oposto (em vermelho) forma a base deste triângulo retângulo. Ou seja, o inverso da situação com o ângulo alfa.
O Cateto adjacente está próximo ao ângulo beta, e o Cateto oposto, está oposto à ele.
Tendo em mente os elementos principais de um triângulo retângulo que são em resumo, seus dois catetos (adjacente e oposto), a hipotenusa, um ângulo reto de 90 graus e dois ângulos agudos chamados de alfa e beta, podemos aprender as relações trigonométricas de um triângulo retângulo:

Relações trigonométricas de um triângulo retângulo:

As relações trigonométricas dos triângulos retângulos são primordiais para efetuarmos mais facilmente os cálculos dos lados de triângulos retângulos, são eles: Seno(sen), Cosseno(Cos) e a Tangente(Tg).
Cada um deles possui uma relação direta dos ângulos agudos do triângulo retângulo, com seus outros elementos.
O Seno relaciona o ângulo agudo com a razão (divisão) entre um Cateto Oposto e a Hipotenusa. Veja esta representação na fórmula:

Aqui estamos dizendo que o Seno do ângulo alfa é igual ao Cateto Oposto dividido pela Hipotenusa.
*No caso de querer relacionar o ângulo beta, basta substituir o ''A'' na fórmula por "B".

Já o Cosseno relaciona o ângulo agudo pela razão (divisão) entre o Cateto Adjacente e a Hipotenusa:

Neste caso estamos dizendo que o Cosseno de alfa é igual à divisão entre Cateto adjacente e a Hipotenusa.

Por fim, temos a Tangente que relacionado o ângulo agudo com os catetos:

Tangente de alfa é igual à Cateto oposto sobre Cateto adjacente.

Vamos à um exemplo para o esclarecimento do uso dessas fórmulas e relações?

Examine o triângulo retângulo abaixo:

Como podemos aplicar esses valores dados nas fórmulas do Seno, Cosseno e Tangente?
Bom, primeiramente basta identificarmos cada elemento, vejamos:

O número 15 está ao oposto do ângulo reto, logo, ele é nossa hipotenusa. Já nos casos dos números 9 e 12, podemos concluir que eles são os catetos, pois formam os cantos deste triângulo retângulo. E como representado na figura, nosso ângulo alfa é igual à 30 graus e nosso ângulo beta igual à 60 graus.
Pronto! Já sabemos quem é quem nessa bagunça! Mas e agora? Como representá-los nas fórmulas?

Se queremos a relação entre os elementos deste triângulo retângulo e o ângulo alfa, basta dizermos que o 12 é o Cateto adjacente e o 9 o Cateto Oposto, pois como visto anteriormente, o Cateto adjacente é o cateto próximo ao ângulo referido, e o Cateto oposto, o cateto que está oposto ao ângulo referido.
Logo, o Seno de alfa(30 graus) ficaria assim:

Pois o Seno relaciona o ângulo referido à divisão entre Cateto Oposto e Hipotenusa.
Cosseno de alfa:

Cosseno relaciona o ângulo referido à divisão entre Cateto Adjacente e Hipotenusa.
Por fim, a Tangente de alfa:

A Tangente relaciona o ângulo referido à divisão entre Cateto Oposto e Cateto Adjacente.

Para relacionar os elementos com o ângulo beta, basta fazer o mesmo processo, só que substituir o ângulo referido nas fórmulas. Se antes era ângulo alfa = 30°, agora será ângulo beta = 60°
Vale lembrar também que: Se para alfa um cateto é adjacente, para beta ele é oposto, e vice-versa:

Vamos à mais um exemplo para praticarmos mais:

Examine este outro triângulo retângulo:

Sim, este também é um triângulo retângulo, porém um pouco mais difícil de ser observado, mas não impossível:
Lembrando que a Hipotenusa sempre estará oposta ao ângulo reto, percebemos que neste caso, nossa hipotenusa é o lado Y, veja:

Ou também o lado maior do triângulo.
Pois bem, se Y é a hipotenusa, nos resta dizer que lado X e lado Z são os catetos, mas quem é adjacente e quem é oposto ao ângulo alfa?
Se você for perceber bem a figura, o X está mais próximo ao ângulo agudo alfa que Z, logo, o X é o Cateto adjacente e o Z o Cateto oposto:

Então agora sabemos quem é quem! Basta apenas substituí-los nas fórmulas das relações:

Depois desses exemplos é fundamental que nesta altura do campeonato você já saiba como identificar os elementos de um triângulo retângulo e suas aplicações nas fórmulas das relações! Mas caso reste alguma dúvida, tente re-ler a aula com mais calma para não ficar com mais nenhuma dúvida, pois agora iremos avançar mais um pouco.

Sabendo identificar os elementos dos triângulos retângulos, e aplicá-los corretamente nas nossas três fórmulas, podemos agora finalmente calcularmos as medidas de cada lado de um triângulo retângulo! Mas antes disso, devemos conhecer alguns números que podem substituir o valor dos ângulos nas nossas fórmulas, veja agora:

Arcos Notáveis:
Na trigonometria, existe uma grande tabela que nos fornece os números que podemos substituir nos ângulos agudos de nossas fórmulas de relações.
A tabela é bem grande e não é necessário decorá-la, mas se quiser ter acesso à ela, clique aqui! 
Esta tabela é muito útil, pois ela nos informa o número a ser substituído, de acordo com cada ângulo agudo do triângulo retângulo e em qual fórmula ele é utilizado.
Porém, na maioria dos problemas envolvendo triângulos retângulos, é muito comum utilizarmos os ângulos de 30 graus, 45 graus e 60 graus.
Eles são chamados de Arcos Notáveis, pois temos uma tabela especial só para eles que é moleza de decorar:

Esta tabela nos fornece determinados números a serem substituídos de acordo com cada ângulo referido (30°, 45°, 60°) e de acordo também com cada fórmula das relações: Seno, Cosseno e Tangente.
O que? Não achou a tabela fácil de decorar? E se você mudar de ideia vendo a construção desta tabela? Acho que ficará mais fácil para memorizá-la, não?
Pois bem, temos aqui a tabela vazia:

Partimos do princípio onde todos os números desta tabela (exceto os dois últimos) são frações:

Em Seno e Cosseno, o denominador destas frações é o número dois:

Na linha do Seno, podemos escrever uma sequência de um à três nos numeradores:

Já no Cosseno a sequência é a mesma, só que de três à um:

Agora todos recebem raízes nos numeradores, menos o meio:

Na tangente de 30 graus, também vamos usar raízes! A raiz de três no numerador e o número três sem raiz no denominador:

Para os dois últimos números que não são frações, colocaremos em 45° da tangente o número 1 e em 60° uma raiz de três novamente:

E aqui está nossa tabela dos arcos notáveis! Creio que agora ela não está tão difícil de decorar, certo?

Agora sabendo esta tabela, as fórmulas de relações e os elementos principais do triângulo retângulo, podemos finalmente calcular seus lados:


Calculando os lados do triângulo retângulo:
Depois de toda a parte teórica, vamos agora aprender a calcular qualquer lado de um triângulo retângulo.
A primeira coisa a se pensar quando queremos encontrar as medidas de algum dos lados de um triângulo retângulo qualquer é em qual fórmula o que queremos calcular se relaciona com o que nós temos, exemplo:

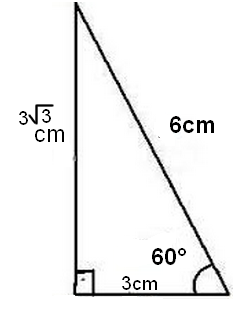
Calcule os Catetos do  triângulo retângulo abaixo, cuja hipotenusa mede 6 cm e o ângulo alfa mede 60 graus:

Como pode notar na imagem acima: Hipotenusa é igual à 6 cm, e o Cateto x é o oposto, enquanto o Cateto Y é adjacente ao ângulo agudo de 60 graus.
Primeiramente iremos encontrar o valor de X, ou seja, do Cateto Oposto.
Se temos a Hipotenusa e queremos encontrar o Cateto Oposto, então já temos uma relação! Mas quem relaciona Cateto oposto com Hipotenusa? Lembra? O Seno!

Substituindo os valores na fórmula temos:

Seno de 60 graus (ângulo fornecido), X = Cateto Oposto e 6 = Hipotenusa!
Verificando na tabela dos arcos notáveis, você pode ver que o Seno de 60 graus é igual à raiz quadrada de 3 sobre 2, então a fórmula fica assim:

Então agora multiplicando em cruz ficamos com: 2x = 6√3
Para isolar o x na equação temos que passar o dois dividindo, então: 

Dividindo os números fora da raiz (6 e 2) temos que 6/2= 3
Logo, x= 3√3
Se quiser encontrar a raiz quadrada de 3 e multiplicar este valor por 3, não tem problema algum, mas deixar o resultado como x= 3√3 também é correto, a não ser que o problema tenha pedido as medidas exatas, o que não é o caso.
Mesmo assim:  3√3 = Aproximadamente: 5,196cm
Se o X era o Cateto Oposto, logo sabemos que o Cateto Oposto deste triângulo retângulo vale 3√3 ou aproximadamente 5,196cm.
Mas e o Cateto Adjacente?
Para isso, basta seguir o mesmo raciocínio, só que agora tente pensar... Quem relaciona Hipotenusa (o que nós temos) com Cateto Adjacente(o que queremos encontrar)? Cosseno!
Então seguindo a fórmula:

Temos que substituir os valores na fórmula, sendo que: ângulo agudo = 60°, Hipotenusa = 6 cm e Cateto Adjacente = Y

Verificando na tabela dos arcos notáveis, Cosseno de 60 é igual à meio, então:

Multiplicando cruzado temos que: 2y= 6
Isolando Y na equação teremos: Y=  6/2 = 3
Logo, Y = 3cm
Então o Cateto adjacente deste triângulo retângulo é igual à 3 cm.
Nosso desenho do triângulo retângulo fica assim:

Outro exemplo mais complexo:

Algumas vezes o problema não nos fornece todas as informações, como por exemplo o ângulo agudo e suas posições no triângulo retângulo, com isto devemos raciocinar um pouco e tentar encontrar quem é quem.
Por exemplo, se foi no fornecido que um dos ângulos mede 30 graus, quanto mede o outro ângulo?
Para isso, basta lembrar que: A soma de todos os três ângulos internos de um triângulo retângulo deve ser igual à 180 graus.
Se já temos um ângulo reto que sempre medirá 90 graus, e mais um de 30 graus, qual será a medida do terceiro? Para isso,  basta fazer uma pequena equação de primeiro grau, onde 'x' é o terceiro ângulo que queremos achar.
x + 90° + 30°= 180°
Isolando ''X'' na equação ficamos com: x = 180° - 90° - 30° -> X = 60° Então nosso terceiro ângulo agudo é de 60 graus! Se você for somar agora os três ângulos internos, dará 180 graus! Logo, a equação é verdadeira! 90° + 30° + 60° = 180°
Vamos ao exemplo:

Calcule os Catetos de um triângulo retângulo, cuja hipotenusa é 2,5 cm e um dos ângulos é igual à 60°:

Primeiramente não sabemos as medidas dos Catetos, logo um deles recebe o nome de X e o outro recebe o nome de Y.
Sabemos também que a Hipotenusa mede 2,5 cm e um dos ângulos é de 60 graus, chamamos então este ângulo de ângulo alfa.
Para encontrarmos o ângulo beta, basta fazer a equação do primeiro grau, onde b = beta:
b + 60° + 90° = 180° -> b = 180° - 60° - 90° -> b = 30°
Logo, nosso ângulo beta é de 30 graus.
Agora que sabemos quem são nossos ângulos, podemos encontrar os Catetos:
Vamos usar a lei dos Senos para ambos, mas se usar a lei do Cosseno também dará certo:
*Por que usar as leis de Seno e Cosseno? Porque ambos relacionam Catetos com Hipotenusa.

Primeiro Cateto = x  Primeiro ângulo dado = 60° então:

Na tabela dos arcos notáveis, o Seno de 60 graus é igual à raiz de 3 sobre dois, logo:

Multiplicando em cruz ficamos com: 2x = 2,5√3
Isolando X na equação: x = 2,5√3 sobre 2. Dividindo os números fora da raiz (2,5 e 2) ficamos com: 1,25√3
Então um dos Catetos mede 1,25√3 cm. Se quiser eliminar esta raiz quadrada, basta multiplicar o 1,25 pela raiz de três que dará aproximadamente 2,165 cm.

Agora iremos encontrar nosso segundo Cateto e já que estamos usando a lei do Seno novamente, usaremos o ângulo beta agora:
Ângulo beta = 30 graus, então:

Na tabela dos arcos notáveis sabe-se que o Seno de 30° é igual à meio, logo ficamos com:

Multiplicando cruzado temos: 2y= 2,5
Isolando Y na equação: y =2,5/2 = 1,25
Logo nosso outro Cateto é igual à 1,25 cm.
Então Cateto x = aproximadamente 2,165 cm e Cateto y = 1,25 cm
Se tem dúvidas com relação às respostas fornecidas, aplique o Teorema de Pitágoras para conferir sua resposta:
O Teorema de Pitágoras diz que: h² = L² + L²
Ou seja, o quadrado da Hipotenusa é igual à soma dos Catetos ao quadrado:
Se a Hipotenusa é igual à 2,5 cm, seu quadrado é igual à 6,25 cm.
Então a soma do quadrado desses dois Catetos deve dar aproximadamente 6,25. Veremos:
(2,165²) + (1,25²)
4,687225 + 1,5625 =  aproximadamente 6,24
Confere! Logo, nossos cálculos estão exatos!


E como posso calcular a área de um triângulo retângulo?
Para calcular a área de qualquer triângulo, você deve multiplicar a base pela altura do triângulo e dividir esse resultado por dois.
No caso do triângulo retângulo, podemos dizer que A= (C.C)/2 
Onde A é a área, C são os dois catetos do triângulo retângulo, tudo isso dividido por 2, exemplo:

Calcule a área de um triângulo retângulo em que seus catetos medem respectivamente 4 m e 6 m:

Se nossos catetos medem 4 metros e 6 metros, já podemos aplicá-los na nossa fórmula da área:
A = (4.6)/2
A = 24/2
A = 12 m²
Logo, a área deste triângulo retângulo é de 12 metros quadrados.