Raízes: Radiciação e Radicalização ~ Aulas da May

Raiz Quadrada:

O que é a Raiz Quadrada?

Para entender melhor o conceito de raízes em matemática, primeiramente conheça a definição de uma raiz quadrada.

Uma raiz quadrada pode ser escrita da seguinte forma: √4

O que estamos dizendo com isto? Estamos dizendo que, como a raiz é quadrada, então um número qualquer ao quadrado é igual à 4. Mas como assim um número qualquer ao quadrado? O que é um número ao quadrado? Não se lembra? Um número ao quadrado quer dizer que ele está sendo multiplicado por ele mesmo duas vezes, ou seja, ao quadrado.
Logo, √4 quer dizer que um número qualquer multiplicado por ele mesmo duas vezes dará quatro! Mas que número é esse? Que número que multiplicado por ele mesmo duas vezes dá quatro? Hum... Essa é fácil de descobrir! É o número 2! Veja: 2.2 = 4. Então dizemos que a raiz quadrada de 4 é igual à 2.
√4 = 2
Se você for pensar também... O número -2 também pode ser a raiz quadrada de quatro, pois veja: (-2) . (-2) = 4, de acordo com a regra dos sinais, menos com menos dá mais, logo o número quatro possui duas raízes: 2 e -2, então podemos dizer que: √4 = ±2 que significa mais ou menos 2.
Veja mais algumas raízes quadradas fáceis de descobrir: √9; √16; √64
Raiz quadrada de 9? Que número ao quadrado dará nove? Ahá! O número 3 -> 3² = 3.3 = 9 e também - 3 -> (-3)² = (-3) . (-3) = 9
E 16? Raiz quadrada de 16 é 4 e consequentemente -4, veja: 4² = 4.4 = 16 e (-4)² = 16! De 64 é mais ou menos 8, olhe: 8² = 8.8 = 64 e (-8)² = 64
Então: √9= ±3; √16= ±4; √64= ±8.
Mas cada um desses elementos na raiz quadrada possui um nome, veja só a nomenclatura de cada elemento de uma raiz:

Nomenclatura:

$\sqrt[n]{{a}^{m}}= b$

Vamos por partes:

n = Índice. Como assim índice?

Toda raiz quadrada significa que um número qualquer multiplicado duas vezes por ele mesmo dará um outro número, certo!? Mas não existe apenas a raiz quadrada na matemática! Temos a raiz cubica, a raiz quarta, raiz quinta, e assim por diante... Ou seja, numa raiz cubica estaremos dizendo que um número qualquer multiplicado por ele mesmo três vezes dará outro número.

Então quando não temos nada no índice, estamos afirmando que ela então é uma raiz quadrada, como neste exemplo: √4

Não há nada no índice, mas poderíamos escrever esta raiz desta forma também: ²√4

Porém, na matemática costumamos considerar raízes quadradas, aquelas raízes que possuem seu índice oculto, ou seja, você não precisa escrever o número 2 num índice de raiz quadrada.

Mas no caso da raiz cubica, por exemplo, o índice deve ser escrito: ³√8 Isso é uma raiz cubica de 8, ou seja, um número qualquer multiplicado por ele mesmo três vezes dará 8.

Então em resumo, o índice é o número que indica que raiz estamos calculando, seja ela quadrada, cubica, quarta, quinta, sexta, e etc...

Continuando com os nomes dos elementos:

√ Chama-se de Radical. Algumas pessoas confundem este símbolo e o chamam de ''raiz'', quando seu verdadeiro nome é radical.

A -> Ou seja, o número dentro do radical, possui o nome de Radicando.

B -> Ou seja, o resultado da operação têm o nome de raiz!

Então para facilitar, analise o número à seguir: √25 =± 5

Uma raiz com índice dois e radicando 25 dará uma raiz de mais ou menos 5! Perceba as nomenclaturas!
Mas claro, isso foi um exemplo para você entender quem é quem numa raiz, o mais correto é afirmar que a raiz quadrada de 25 é igual à mais ou menos 5.

m -> É o expoente do radicando, por exemplo: √10², onde no caso aqui, o número dois nesta potência é o expoente de 10, que é o radicando.

Mas por enquanto você aprendeu a encontrar raízes quadradas de números fáceis e bem óbvios, mas e se eu te pedir para que você encontre a raiz quadrada de 2? √2 = ?

Método da Aproximação:

Mas raiz quadrada de 2 -> √2 significa que um número deve ser multiplicado por ele mesmo duas vezes para dar dois! Mas não existe nenhum número inteiro que multiplicado por ele duas vezes dará dois! O menor número que conheço antes do 2 é o 1, e 1.1 = 1. Então 2 não tem raiz quadrada?
Errado! O 2 possui raiz quadrada sim, só que ele não é um número inteiro, e sim um número irracional! Ou seja, não será algo exato à dois, e sim aproximado, pois estamos tratando de números decimais(quebrados).
Então pense... Que número decimal pode estar entre 1(menor que dois) e o dois? (pois queremos algum número que chegue perto de 2, não que o ultrapasse, por isso esse número deve estar entre 1 que é um número menor que dois, e o próprio dois).
0,1 é o primeiro número a saber pensando mas 0,1 é um número MUITO baixo com relação ao número dois, então partimos para o pensamento de algo maior como 1,0. Porém, 1,0 é o mesmo que escrever 1, e 1.1 como já visto dará 1, então o próximo a ser pensado é o 1,1!
Veja bem, se você multiplicar 1,1 por ele mesmo você terá o resultado de 1,21! Um número bem baixo quando queremos saber a raiz quadrada de 2, não? Então o que você deve fazer? Utilizar o método da aproximação para raízes de números primos(números primos são aqueles números que só são divisíveis por eles mesmos ou por 1)
Se 1,1² é um número baixo e não muito próximo à dois, como devemos proceder? Vamos aumentando o valor da última casa decimal, até encontrarmos o que queremos: 1,1² não é, então vamos fazer 1,2²: 1,44! Ainda é um valor muito baixo e estamos percebendo que multiplicar o número 1 com mais uma unidade na casa decimal não está sendo muito suscetivo, então a melhor saída é adicionar mais um casa decimal: 1,11² chegamos ao resultado de 1,2321! Melhorou, mas ainda não é o que precisamos, vamos aumentar mais um pouco! 1,21² = 1,4641! Ainda não... Aumentaremos mais: 1,31² = 1,7161! Está mais perto mas ainda não é isso! 1,41² = 1,9881! Opa! Parece que agora estamos bem perto! E se tentarmos 1,42²!? Dará 2,0164! Um número um pouco maior que 2! E queremos a raiz quadrada de dois aproximadamente e não um número que ultrapasse 2, logo, o número mais próximo para ser raiz de 2 é 1,41, e claro, consequentemente -1,41.
√2 ≅ ± 1,41
O mesmo pode ocorrer com as raízes de 3, de 5, 7, 11, 13 e etc... Pois todos eles são números primos.
Quando se trata de números primos o único método existente para encontrar sua raiz, é utilizando o método da aproximação.
Mas não se preocupe! Com números não primos temos um método mais eficaz de encontramos suas raízes referentes, sem ter que utilizar o método da aproximação! Mas isso é mais para frente na aula!

Observações*

* A raiz de 1 sempre será 1, independente do índice, veja: √1 = 1 pois: 1.1= 1

pois: 1.1.1.1 = 4

Dará 1 pois: 1 vezes ele mesmo quinhentas vezes dará 1.

* O mesmo ocorre com o zero, pois zero multiplicado por ele mesmo dará zero: ³√0 =0

* Quando o índice do radical for igual a um, o resultado da raiz será o próprio radicando: ¹√35 = 35, ¹√6 = 6, ¹√70000 = 70000.
Isso ocorre porque o índice indica quantas vezes o número dentro do radical está sendo multiplicado, se o índice for um, isso indica que o número está sendo multiplicado apenas uma vez, o que resulta no próprio número.

* Quando o índice for zero, a raiz não existe, pois é impossível dizer que um número está sendo multiplicado zero vezes.

* No conjunto dos números reais não existe raiz quadrada com radicando negativo, pois √-16 por exemplo, significa que um número qualquer deve ser multiplicado por ele mesmo duas vezes até dar 16, porém, o único número multiplicado por ele mesmo duas vezes que dará 16 é o 4 -> 4.4 = 16

O menos 4 (-4) também dará 16 positivo, veja: (-4).(-4) = 16, pois através da regra dos sinais, negativo com negativo é igual à positivo!

Logo, para os números reais √-x não existe! Isso é uma assunto a ser discutido em outra aula (números complexos,onde aí sim um radicando pode ser menor que zero) Mas por enquanto √-x não existe.

Raízes com índice diferente de 2:
Então, como visto superficialmente no início da aula, uma raiz não precisa ser sempre quadrada, ou seja, com o índice oculto, temos os casos de raízes com índices diferentes de 2, como por exemplo a raiz cubica ou raiz quarta, e etc...Veja só um exemplo:
Qual a diferença entre: √8 e ³√8?
Bem, no primeiro caso temos que descobrir a raiz quadrada de 8, ou seja, um número que ao quadrado dará 8. E se você for reparar bem, nenhum número inteiro multiplicado duas vezes por ele mesmo dará 8, então com o que você aprendeu até aqui, devemos utilizar o método da aproximação para descobrirmos a raiz quadrada de 8, logo, ela(raiz) será um número decimal e não exato à 8. Já a raiz cubica de 8 toma outro rumo, porque aqui nós estamos dizendo que um número multiplicado por ele mesmo três vezes deverá dar 8.
Se 2² = 4 quanto seria 2³? 2. 2. 2? 8, certo? Então neste caso, um número ao cubo que pode resultar em 8 é o 2, pois 2³ = 8.
Mas (-2)³ não pode ser raiz de oito positivo, pois: (-2)³ = (-2). (-2). (-2) = -8, seguindo a regra dos sinais. Por isso, a raiz cubica de 8 só pode ser um número, no caso, o 2.

Observação*
* Diferente do caso da raiz quadrada, um radicando pode ser um número negativo, desde que seu índice seja um número ímpar, por exemplo: ³√-512 ou

No caso de um índice ser um número par, ter um radicando negativo é um absurdo no conjunto dos números reais, pois nenhuma potência de base positiva, poderá resultar num número negativo!

* Raízes de índices pares sempre resultarão em dois resultados, já raízes com números ímpares, só resultará uma raiz.

E você? Sabe me dizer as raízes cubicas de: ³√27; ³√64; ³√125 e ³√-216?

³√27 = 3 pois: 3³ = 27
³√64 = 4 pois: 4³ = 64
³√125 = 5 pois: 5³ = 125
³√-216 = -6, pois (-6)³ = - 216

E existem raízes com infinitos índices como raiz sexta

raiz de 20, raiz de 1000 e assim por diante...
Porém, como você pode notar, quanto maior o índice, maior o seu radicando, e tentar descobrir raízes de números com índices ou radicando muito altos apenas com o método da aproximação pode ser um trabalho árduo e não muito eficiente, por isto nós temos um método alternativo quando trabalhamos com raízes! O método da radiciação!

Radiciação:
A radiciação é uma operação matemática que trabalha principalmente com raízes e pode facilitar nossos cálculos envolvendo as mesmas.
Na Radiciação encontramos algumas propriedades fundamentais, são elas:

Propriedade 1:
A raiz de uma potência é o radicando que passa a ser um número fora do radical com uma potência de expoente fracionário.
Isso se o radicando for maior ou igual à zero e o índice diferente de zero:

$\sqrt[n]{{a}^{m}}= {a}^{\frac{m}{n}}$ (a ≥ 0 e n ≠ 0)

Por exemplo:

Se temos um expoente no radicando, podemos sempre pensar assim: "O expoente será o numerador da fração e o índice será o denominador''.
Como assim? Nós iremos pegar o expoente do radicando, no caso o 10, e iremos colocá-lo como numerador de uma fração. Já o índice 5 será o denominador.
Logo, o 3 poderá ''sair'' da raiz e teremos: ${3}^{\frac{10}{5}}$
Com um expoente fracionário é fácil de trabalhar,basta simplificá-lo que teremos um resultado mais preciso, no caso aqui temos uma fração:

e então basta dividir o numerador pelo denominador que teremos o resultado de 2, pois 10/5=2

Então nós ficamos com 3².
3 ao quadrado é 9, logo: $\sqrt[5]{{3}^{10}}= 9$

Outro exemplo:
$\sqrt[3]{{4}^{15}}$
Se o expoente do radicando é o numerador e o índice é o denominador, então temos: ${4}^{\frac{15}{3}}$
Dividindo 15 por 3 teremos 5: 15/3=5
Então ficamos com ${4}^{5}$ .
Logo: $\sqrt[3]{{4}^{15}} = {4}^{5}$

E se o expoente for um número decimal? Mesmo processo, exemplo:
$\sqrt[]{{2}^{0,5}}$

Temos que transformar o 0,5 numa fração! Se temos apenas uma casa decimal após a vírgula, então temos 10 como denominador e 5 como numerador (veja a aula sobre estas conversões) logo, 2 sai da raiz e ficamos com: ${2}^{\frac{5}{10}$ simplificando essa fração por 5, teremos: ${2}^{\frac{1}{2}$ pois 5/5 = 1; 10/5=2
${2}^{\frac{1}{2}$ é o nosso resultado, mas podemos ir mas além... Pense... se temos ${2}^{\frac{1}{2}$ isso quer dizer que se transformarmos essa número numa fração, teremos $\sqrt[]{2}$ . Por que? Veja bem, se o denominador da fração é o índice de uma raiz e o numerador o expoente, com ${2}^{\frac{1}{2}$ temos 1 como numerador que pode se tornar expoente, e 2 como denominador que pode se tornar índice, logo ${2}^{\frac{1}{2}$ = $\sqrt[]{2}$ , o 1 que é expoente pode ficar oculto, porque numa potência o 1 não precisa ser escrito, e o 2 também fica oculto porque numa raiz quadrada o índice não precisa ser escrito, mas sabemos que vale 2. Em resumo ${2}^{\frac{1}{2}$ é o mesmo que raiz quadrada de 2. Ambas respostas estão corretas.
Outro exemplo:

$\sqrt[6]{{2}^{3}}$ expoente vira numerador, e índice denominador, logo, 2 sai da raiz e ficamos com: ${2}^{\frac{3}{6}}$ . Simplifique essa fração por 3: 3/3 =1; 6/3 = 2, logo novamente temos: ${2}^{\frac{1}{2}}$ que é também: $\sqrt[]{2}$
Logo, $\sqrt[6]{{2}^{3}}$ = $\sqrt[]{2}$

E o que pode acontecer se o índice da raiz for um número fracionário? Por exemplo:

$\sqrt[\frac{8}{4}]{{24}^{2}}$

Nesse caso, iremos utilizar ainda essa propriedade, veja como se resolve um caso desse:

À partir desta propriedade, sabemos que o expoente do radicando será o numerador da fração, e o índice da raiz será o denominador, então:

$\sqrt[\frac{8}{4}]{{24}^{2}} \rightarrow {24}^{\frac{2}{\frac{8}{4}}}$

Se está com dificuldades para enxergar o expoente desta potência, ele está assim: ${\frac{2}{\frac{8}{4}}$

Esqueceremos por enquanto o número 24, e vamos nos atentar a resolver o expoente.
Agora devemos aplicar a propriedade da divisão entre frações: Essa propriedade nos diz que: Quando temos uma divisão entre frações, temos também uma multiplicação entre elas, contanto que conservemos o primeiro fator e multipliquemos pelo segundo com a ordem invertida, ou seja, quem é numerador passa a ser denominador e quem é denominador vira numerador:

${\frac{2}{\frac{8}{4}}$

Para deixar essa fração mais correta, vamos adicionar um denominador 1 para o 2:

$\frac{\frac{2}{1}}{\frac{8}{4}}$

Agora podemos aplicar a propriedade das divisões de frações:

Conserve o primeiro (2/1) e multiplique pelo segundo com a ordem invertida: (8/4) --> 4/8:

$\frac{\frac{2}{1}}{\frac{8}{4}} \rightarrow \frac{2}{1} * \frac{4}{8}$

Basta agora multiplicar tudo:

$\frac{2}{1} * \frac{4}{8} = \frac{8}{8} = 1$

E aí está: 24¹ ou 24

O mesmo pode ocorrer quando temos um expoente fracionário:

$\sqrt[7]{{55}^{\frac{2}{3}}}$

Utilizando a propriedade 1 temos:

$\sqrt[7]{{55}^{\frac{2}{3}}} \rightarrow {55}^{\frac{2}{\frac{3}{7}}}$

Basta aplicar a propriedade da divisão entre frações já apresentada:

${\frac{2}{\frac{3}{7}}} = \frac{2}{3} * \frac{1}{7} = \frac{2}{21}$

Por fim temos:

${55}^{\frac{2}{21}}$

E quando temos um número decimal (tanto no índice quanto no expoente do radicando) o preferível é torná-lo uma fração:

$\sqrt[2,3]{44} \rightarrow \sqrt[\frac{23}{10}]{44}\, e\,\,\, \sqrt[]{{3}^{0,09}} \rightarrow \sqrt[]{{3}^{\frac{9}{100}}}$

Propriedade 2:
$(\sqrt[n]{a})^{m} = \sqrt[n]{{a}^{m}}$
Quando temos o caso de uma potência numa raiz, podemos inserir esse expoente que está fora do radical, e passar a adotá-lo como o expoente do radicando:

$(\sqrt[6]{64})^{12}$

No caso aqui, podemos passar esse expoente 12 para dentro do radical, e torná-lo o expoente do radicando 64:

$\sqrt[6]{{64}^{12}}$

Agora basta radiciar à partir da primeira propriedade:

$\sqrt[6]{{64}^{12}} \rightarrow {64}^{\frac{12}{6}} \rightarrow {64}^{2} \rightarrow 4096$

Outro exemplo:

$(\sqrt[3]{2})³$ Aqui, basta você passar o expoente fora dos parênteses, para dentro do radicando, e teremos:
$\sqrt[3]{{2}^{3}}$ , utilizando a propriedade 1: Expoente numerador da fração, índice denominador: ${2}^{\frac{3}{3}}$ . Divida numerador pelo denominador e teremos 2¹ ou 2. Logo:

= 2
Outro exemplo:

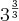$(5\sqrt[3]{3})³$ -> Passe o expoente 3 para o radicando para termos: $5\sqrt[3]{{3}^{3}}}$ o 5 por enquanto não nos importa, o importante é radiciar a raiz cubica de 3 ao cubo $\sqrt[3]{{3}^{3}}$ Siga a propriedade 1 e teremos: ${3}^{\frac{3}{3}}$ que simplificando ficará 3¹ ou 3. Agora $5\sqrt[3]{{3}^{3}}$ se tornou ${5}^{3}. 3$ e esse já seria o resultado correto, mas se quiser, basta fazer 5 ao cubo, vezes 3 que dará: 5³ = 125
125. 3 = 375
Logo, $(5\sqrt[3]{3})³ = 375$

No caso de termos já um expoente no radicando, basta então multiplicar esse expoente do radicando, com o expoente fora da raiz, seguindo a propriedade da potenciação:

$(\sqrt[5]{{890}^{10}})^{2} \rightarrow \sqrt[5]{{890}^{10*2}} \rightarrow \sqrt[5]{{890}^{20}}$

Agora basta radiciar à partir da primeira propriedade:

$\sqrt[5]{{890}^{20}} = {890}^{\frac{20}{5}} = {890}^{4}$

Propriedade 3:
$\sqrt[n]{\frac{a}{b}} \rightarrow \frac{\sqrt[n]{a}}{\sqrt[n]{b}}$
De um modo geral, na divisão de radicais de mesmo índice, mantemos o índice e dividimos os radicais.
Exemplos:

$\sqrt[]{\frac{8}{2}}$ divida 8 por 2 e terás: $\sqrt[]{4}$ Raiz quadrada de 4 você já sabe: 2
Então: $\sqrt[]{\frac{8}{2}} = 2$

Outro exemplo: $\sqrt[]{\frac{27}{3}}$ -> Divida 27 por 3 e obtenha: $\sqrt[]{9}$ raiz quadrada de 9 é 3, logo:
$\sqrt[]{\frac{27}{3}} = 3$

E mais outro exemplo: $\sqrt[3]{\frac{16}{2}}$ -> mesmo processo mesmo o índice sendo 3 agora: divida 16 por 2 e terás: $\sqrt[3]{8}$ -> Raiz cubica de 8, como passado no começo dessa aula é igual à 2, pois: 2³ = 2.2.2 = 8
Logo: $\sqrt[3]{\frac{16}{2}} = 2$

Mas, e se o numerador não for divisível pelo denominador? Daí, basta você ''quebrar'' a raiz em duas:

$\sqrt[]{\frac{4}{9}}$ quebrando essa raiz, teremos uma raiz de 4 e outra de 9, veja: $\frac{\sqrt[]{4}}{\sqrt[]{9}}$ raiz quadrada de 4 como está cansado de saber é 2 e raiz quadrada de 9 é 3, logo teremos: $\frac{2}{3}$ não dá para simplificar, então ficamos com isso mesmo: $\sqrt[]{\frac{4}{9}}$ = $\frac{2}{3}$

Mais outro exemplo:

$\sqrt[3]{\frac{{2}^{3}}{{4}^{6}}}$ Aqui o caso parece ser mais complicado mas não é, basta aplicar a Propriedade 3 e a Propriedade 1 aqui, e tudo ficará certo.
Se temos uma divisão de uma raiz de mesmo índice, e sabemos que o numerador 2 não pode dividir o denominador 4, basta ''quebrar'' essas raízes, mantendo sempre o mesmo índice:

$\frac{\sqrt[3]{{2}^{3}}}{\sqrt[3]{{4}^{6}}}$ Agora vamos radiciá-las, separadamente, primeiro o numerador $\sqrt[3]{{2}^{3}}$ . Aplique a propriedade 1, onde expoente torna-se numerador e índice torna-se denominador: ${2}^{\frac{3}{3}}$ -> ${2}^{1}$ ->

Então nosso numerador é 2, não se esqueça dele, e vamos radiciar o denominador: $\sqrt[3]{{4}^{6}}$
Lembre-se sempre da propriedade 1 da radiciação: expoente do radicando vira numerador, e índice da raiz vira numerador, com isso temos 4 fora da raiz e : ${4}^{\frac{6}{3}}$ divida 6 por 3 na potência e fique com 2, logo: ${4}^{2}$ que é 16, pois 4² = 4.4= 16
Então temos a seguinte fração: $\frac{2}{16}$ que simplificando por 2 iremos obter: $\frac{1}{8}$
Logo: $\sqrt[3]{\frac{{2}^{3}}{{4}^{6}}}= \frac{1}{8}$

E nesse caso: $\sqrt[]{0,01}$ você me diria que isso seria um caso para a propriedade 3 e divisões?
Claro que é, se quisermos transformar esse decimal numa fração! Lembra da conversão? Quantos números temos após a vírgula? dois? Então teremos o 100 com denominador e o 1 como numerador, logo podemos dizer que: $\sqrt[]{0,01} = \sqrt[]{\frac{1}{100}}$
Bastando aplicar a propriedade 3 teremos: $\frac{\sqrt[]{1}}{\sqrt[]{100}}$ raiz de 1 sabemos que é o próprio 1 (vide início da aula) e raiz de 100 é 10, então sabendo as raízes de ambos, teremos: $\frac{1}{10}$

Logo: $\sqrt[]{0,01} = \frac{1}{10}$

Sabemos que é possível aplicar esse métodos com raízes de índices similares, mas e se um índice for diferente do outro?
Se os índices forem diferentes basta fatorá-los, para reduzi-los num só índice, para podermos aplicar a propriedade 3:

$\frac{\sqrt[9]{{2}^{3}}}{\sqrt[3]{{8}^{6}}}$ -> Aqui nós temos os índices 9 e 3, para fatorá-los, basta tirar o MMC de ambos:

9, 3 | 3
3, 1 | 3
1 3.3 = 9
Então agora nosso índice torna-se um só: $\sqrt[9]{\frac{{2}^{3}}{{8}^{6}}}= \frac{\sqrt[9]{{2}^{3}}}{\sqrt[9]{{8}^{6}}}$
Vamos radiciar cada um dos números, começando pelo numerador: ${\sqrt[9]{{2}^{3}}$ , aplicando a propriedade 1 temos que: ${2}^{\frac{3}{9}}$ que simplificando o expoente da potência por 3 fica: ${2}^{\frac{1}{3}}$ , então esse é o nosso numerador, ou transformando esse número numa raiz, pegando o numerador da potência e transformando no expoente do radicando, e o denominador da potência e transformando no índice de uma raiz teremos: $\sqrt[3]{2}$
Vamos agora radiciar o nosso segundo número: $\sqrt[9]{{8}^{6}}$ -> Radiciando com a propriedade 1:
${8}^{\frac{6}{9}}$ Simplificando o expoente da potência por 3 -> ${8}^{\frac{2}{3}}$

Então nossa fração fica assim: $\frac{\sqrt[3]{2}}{{8}^{\frac{2}{3}}}$

Resultado final: $\frac{\sqrt[9]{{2}^{3}}}{\sqrt[3]{{8}^{6}}}$ = $\frac{\sqrt[3]{2}}{{8}^{\frac{2}{3}}}$

Outro exemplo:

$\frac{\sqrt[]{5}}{\sqrt[3]{4}}$ Aqui os índices são diferentes pois no numerador temos uma raiz quadrada de 5 (índice oculto) e no denominador uma raiz cubica de 4.
Vamos primeiro fatorar esses índices de radicais diferentes:

3,2 | 2
3, 1| 3
1 3.2 = 6

Logo, nosso índice ficará: $\frac{\sqrt[6]{5}}{\sqrt[6]{4}}$

E aí está! Se quiser radiciar, fique à vontade.

Propriedade 4:
$\sqrt[m]{\sqrt[n]{a}} \rightarrow \sqrt[m*n]{a}$

No caso de termos uma raiz dentro de outra raiz, basta multiplicamos seus índices para igualá-los:

$\sqrt[3]{\sqrt[5]{18}}$

Aqui faremos 3*5 = 15 e iremos obter:

$\sqrt[3]{\sqrt[5]{18}} \rightarrow \sqrt[3*5]{18} = \sqrt[15]{18}$

Outro exemplo?

$\sqrt[50]{\sqrt[12]{670}} \rightarrow \sqrt[50*12]{670} = \sqrt[600]{670}$

Propriedade 5:

$\sqrt[n]{a * b} \rightarrow \sqrt[n]{a} * \sqrt[n]{b}$

Sempre que tivermos uma multiplicação entre radicandos num mesmo radical, basta separá-los de forma que fiquem cada um num radical diferente, porém com o mesmo índice, e realizar a multiplicação normalmente, sempre mantendo o índice:

$\sqrt[3]{3 * 5}$

Olha só como é simples, basta separar a raiz cubica de 3, com a raiz cubica de 5:

$\sqrt[3]{3 * 5} \rightarrow \sqrt[3]{3} * \sqrt[3]{5}$

Depois é só multiplicar ambos:

$\sqrt[3]{3} * \sqrt[3]{5} = \sqrt[3]{15}$

E aí está! Veja mais esse outro exemplo:

$\sqrt[4]{36 * {5}^{8} * 8}$

Basta separar todos as raízes, mas sempre mantendo o mesmo índice:

$\sqrt[4]{36} * \sqrt[4]{{5}^{8}} * \sqrt[4]{8}$

Agora antes de multiplicar tudo, perceba que a raiz quarta de 5 na oitava possui um expoente, logo, vamos radiciá-lo, utilizando a propriedade 1:

$\sqrt[4]{{5}^{8}} = {5}^{\frac{8}{4}} = {5}^{\frac{2}{1}} = {5}^{2} = 25$

Então temos:

$\sqrt[4]{36} * 25 * \sqrt[4]{8}$

Perceba que o 25 não é mais uma raiz, por tanto, não pode multiplicar diretamente raiz quarta de 8 e raiz quarta de 36. Logo:

$25(\sqrt[4]{8} * \sqrt[4]{36})$

Então ficamos:

$25\sqrt[4]{288}$

Sim, está é a resolução: 25 vezes raiz quarta de 288.

No caso dos índices serem diferentes:

$\sqrt[4]{12} * \sqrt[8]{34} * \sqrt[3]{2}$

Basta tirar o MMC entre eles para igualá-los:

4, 8, 3|2
2, 4, 3|2
1, 2, 3|2
1, 1, 3|3
1, 1, 1

2³.3 = 24

Agora temos:

$\sqrt[24]{12} * \sqrt[24]{34} * \sqrt[24]{2}$

Basta então multiplicar tudo:

$\sqrt[24]{12} * \sqrt[24]{34} * \sqrt[24]{2} = \sqrt[24]{816}$

E no caso de um número vir na frente de uma raiz?

$3\,\sqrt[3]{45} * 5\,\sqrt[3]{12}$

Esse número na frente da raiz tem o nome de coeficiente e para resolver algo como isto, basta multiplicar os coeficiente normalmente, e multiplicar os radicais também:

$15\,\sqrt[3]{540}$

Você aprendeu essa propriedade 5 justamente para conhecer como simplificar raízes, algo que foi prometido logo no inicio da aula!

Simplificação de raízes:
Lembra que no início da aula eu havia prometido como encontrar o valor de uma raiz não exata, ou uma raiz muito grande? Então! A hora chegou!

Vamos ver este exemplo:

$\sqrt[]{144}$

Aqui como temos uma raiz muito grande, podemos fatorar para diminuí-la:

144|2
72 |2
36 |2
18 |2
9 |3
3 |3
1

Depois de fatorar o 144 ficamos com:

${2}^{4} * {3}^{2}$

Lembre-se que esses números ainda são raízes, então:

$\sqrt[]{{2}^{4} * {3}^{2}}$

Aplicando a quinta propriedade temos:

$\sqrt[]{{2}^{4}} * \sqrt[]{{3}^{2}}$

Vamos radiciar cada um deles, à partir da primeira propriedade:

$\sqrt[]{{2}^{4}} \rightarrow {2}^{\frac{4}{2}} \rightarrow {2}^{2} \rightarrow 4$

$\sqrt[]{{3}^{2}} \rightarrow {3}^{\frac{2}{2}} \rightarrow {3}^{1} \rightarrow 3$

4 * 3

Agora basta multiplicar: 4*3 = 12.
Então a raiz quadrada de 144 é igual à 12!
Viu? Encontramos com mais facilidade a raiz de um número grande sem necessitar do método da aproximação, fizemos isso apenas utilizando as propriedades da radiciação ensinadas nesta aula.

Vamos ver outros exemplos?

$\sqrt[3]{56}$

Fatore o 56:

56|2
28|2
14|2
7 |7
1

$\sqrt[3]{{2}^{3} * 7} \rightarrow \sqrt[3]{{2}^{3}} * \sqrt[3]{7}$

Radiciando:

$\sqrt[3]{{2}^{3}} \rightarrow {2}^{\frac{3}{3}} \rightarrow {2}^{1} \rightarrow 2$

$2\, \sqrt[3]{7}$

Note que não sabemos a raiz cúbica de 7 e nem podemos fatorá-lo por se tratar de um número primo, logo a resolução é essa mesmo: $2\, \sqrt[3]{7}$

14 comentários:

João Labrego2 de fevereiro de 2015 às 15:45
Aproveito a oportunidade para deixar aqui um método de radiciação super-simples, eficiente e absolutamente preciso.

Deixo aqui o artigo que escrevi:

UM OLHAR PARA A RADICIAÇÃO

De tanto ver gente desesperada por um algoritmo simples e eficiente que determine radiciações de quaisquer índices, decidi divulgar o algoritmo que uso denominado pelo seu criador como Método Geral da Radiciação.

Eu fico imaginando com meus botões sobre o porquê de ninguém ainda ter descoberto esse método de tão simples que é, afinal, hoje temos cerca de 7 bilhões de seres-humanos no planeta.

Chega de críticas ácidas ao intelecto alheio e vamos logo ao assunto que interessa.

Como sou péssimo desenhista no computador, ao invés de desenhar um radical que é o símbolo da radiciação, vou utilizar-me da expressão root e entre parênteses o valor do radicando e, separado por vírgula, o índice do radical.

Portanto, vamos logo ao exemplo que é isso que nos interessa.

Calculemos a root(123456789, 5), ou seja, a raiz quinta de 123456789.
O primeiro passo é dividirmos o radicando, da direita para a esquerda, em grupos de algarismo de 5 algarismos cada.
1234.56789
Como podem notar, formamos um grupo de 5 algarismos à direita e um de 4 à esquerda.
Determinemos agora o primeiro algarismo da raiz que elevado à quinta potência resulte 1234.
Como eu usei a calculadora do Windows eu encontrei o valor 4.
Logo, o primeiro dígito da raiz será 4.
O segundo dígito será encontrado concatenando-se o próximo dígito ao primeiro e procurando um dígito de 0 a 9 que concatenado à direita do primeiro algarismo da raiz forma um número que elevado à quinta potência resulta 123.456.789.
Confuso? Simples.
Fica assim a nossa expressão: root(123456789, 5) = 4___
Como eu usei a calculadora do Windows encontrei o dígito 1 que concatenado à esquerda do dígito 4 resulta 41.

Elevando-se 41 à quinta potência obtemos 115.856.201 e resto 7.600.588.
Podemos continuar a operação para encontrarmos as casas decimais, tantas quantas quisermos, bastando acrescentar grupos de 5 zeros à direita do radicando para cada casa decimal desejada na raiz.
Vamos calcular 3 casas decimais.
Só para adiantar, o resultado da calculadora é 41,524364578276233587124014318541.
Calculemos então: root(1234.56789.00000.00000.00000)
Observe que acrescentei 15 zeros separados de 5 em 5 dígitos porque quero encontrar a raiz quinta. Se fosse a raiz cúbica seria 3 zeros, quadrada seria 2 zeros, décima seria 10 zeros, e assim por diante.
Para determinarmos o primeiro dígito decimal, tomamos o radicando já calculado 123456789 e o concatenamos com o primeiro grupo de 5 zeros.
Fica assim: root(12345678900000, 5)
Agora, determinemos o dígito que concatenado à direita da raiz já encontrada forma com ele um número que elevado à quinta potência resulte um número próximo ou igual ao radicando.
Seria: 415 pois 415 elevado à quinta potência resulta 12.309.502.009.375 e resto 36.300.347.414.
Observem que não estou utilizando o resto para nada e, portanto, nem precisaria calculá-lo, a não ser no final de toda a operação, caso o mesmo me interesse.
Deixo agora os outros dois dígitos decimais como exercício.
Acho que deu para vocês pegarem o jeito.
Esse método funciona para quaisquer índices de raízes.
Tenho em meu PC uma biblioteca de números gigantes e testei exaustivamente esse algoritmo com números de até 1000 dígitos.
Fiz uma função em C++ com esse algoritmo e um radicando de 10.000 dígitos demorou 14 segundos para ser calculado.
Já com 15.000 dígitos o tempo dobrou, ou seja, 30 segundos.
Com 5.000 dígitos o tempo foi imperceptível, creio que menos de 1 segundo.
A demora se deve ao fato de a cada dígito calculado termos que utilizar no cálculo todo o radicado e toda a raiz já calculada.
Por isso, se o número tem 10.000 dígitos, no final o algoritmo estará multiplicando valores enormes a cada dígito calculado.
No início é super-veloz porque os números são pequenos mas até 5.000 dígitos dá para considerar como um número pequeno ainda, ao menos para esse algoritmo.

By João da Rocha Labrego
ResponderExcluir
Respostas
João Labrego2 de fevereiro de 2015 às 15:53
Somente para se ter uma ideia da importância suprema da divulgação desse algoritmo é que um matemático indiano criou um algoritmo para esta mesma finalidade que além de complexo e demandar mais cálculos, ainda teve a pachorra de patenteá-lo.

Eis o link: http://www.google.com/patents/WO2013068777A2?cl=en
ResponderExcluir
Respostas
Julimar Ferreira6 de fevereiro de 2016 às 19:07
Tem como eu transformar uma raiz nona em raiz cubica
ResponderExcluir
Respostas
Julimar Ferreira17 de fevereiro de 2016 às 13:04
Obrigado mayleone
ResponderExcluir
Respostas
Unknown10 de abril de 2016 às 13:13
Tenho prova amanhã e li e me complicou
ResponderExcluir
Respostas
Unknown23 de abril de 2016 às 06:20
Este comentário foi removido pelo autor.
ResponderExcluir
Respostas
Unknown23 de abril de 2016 às 06:23
Na parte do 5 raiz de Cubica de 3 elevado a 3 ////5v3³ (com o indice 3)//// logo depois o 5 vira 5³ minha duvida é porque o 5 foi elevado a ³ logo depois, me explica que sou novo nessa materia
ResponderExcluir
Respostas
Cida Oliveira16 de outubro de 2016 às 14:39
Adorei sua explicação.Você realmente ensina pra quem não sabe matemática,amei.Quero mais aulas de matematica com vc.
ResponderExcluir
Respostas
Unknown18 de janeiro de 2017 às 13:13
Estás de parabens vc me ajudou, pode enviar esse materia para meu damacuacue@gmail.com
ResponderExcluir
Respostas
Unknown17 de agosto de 2017 às 04:45
Obrigado por teres publicado este artigo me ajudou a entender tudo relacionado com a radicalizaçāo.
ResponderExcluir
Respostas
matematicabasicaaqui7 de julho de 2018 às 03:47
Adorei! Esclareceu muitas coisas pra mim.
ResponderExcluir
Respostas

Adicionar comentário

Aulas da May

domingo, 20 de abril de 2014

Raízes: Radiciação e Radicalização

14 comentários:

Entre em contato: