Teorema de Tales

 Tales de Mileto foi um filósofo e matemático da antiga Grécia no século VI a.C (antes de Cristo).
Ele atribuiu à matemática diversos conhecimentos geométricos à partir de distâncias e suas relações de proporcionalidade.
Ao perceber que os raios solares são paralelos entre si quando incidem a Terra, Tales pôde medir a altura de uma pirâmide no Egito, sem a necessidade de escalá-la!
Ele notou que havia uma proporcionalidade entre as medidas da sombra da pirâmide e de uma estaca que ele havia fincado próximo à essa pirâmide.
Tales então descobriu que se existe uma proporcionalidade entre as sombras desses objetos, há também uma proporcionalidade relacionada às alturas dos mesmos. Logo, sabendo a medida das sombras da estaca e da Pirâmide, que foram formadas à partir dos raios de sol que eram paralelos entre si, e sabendo também a altura da estaca, ele então poderia descobrir a altura da pirâmide à partir dessa relação, sem necessariamente escalá-la!
Foi graças à esse raciocínio que ele desenvolveu o Teorema que leva seu nome, o Teorema de Tales, que até hoje é muito utilizado na matemática e em outras áreas.

Veja um exemplo do que Tales raciocinou:

Note que na imagem acima temos quatro elementos para percebemos:
Em beje a pirâmide e seu segmento de reta em vermelho que representa sua altura; em laranja temos a estaca, e em marrom temos as duas sombras de ambos objetos.
Vamos imaginar que a sombra formada pela pirâmide meça 8 metros, e que a sombra da estaca meça 1,75 metros. Por fim, imagine que a altura dessa estaca seja de 3,5 metros e a altura da pirâmide seja de 16 metros:

Note que há uma proporcionalidade entre as sombras dos objetos e suas alturas: A sombra da estaca é a metade da medida de sua altura: 3,5 divido por 2 = 1,75. 
Com base dessa proporcionalidade, você pode notar que o mesmo acontece com as medidas da pirâmide: Sua sombra é a metade da medida de sua altura (16/2 = 8).
Se temos essa relação de proporcionalidade direta, podemos dizer o seguinte:




Que a altura da pirâmide está para a sua sombra, assim como a altura da estaca está para sua sombra.

Substitua os valores nessa relação e comprove você mesmo:



Agora faça uma regra de três:

16 * 1,75 = 3,5 * 8
28 = 28

E aí? Equação satisfeita, certo? Isso demonstra a verdade da relação!

Veja que com essa razão ou relação de proporcionalidade, podemos descobrir as medidas
de algo que dificulta o acesso de sua altura. Vamos ver um exemplo?

Para medir a altura de um prédio, um rapaz mediu a altura de uma árvore próxima à este prédio, essa árvore media cerca de 2,6 metros de altura. Ele também mediu as sombras do prédio e da árvore e notou que a sombra da árvore media cerca de 1,3 metros e que a sombra do prédio media em torno de 10 metros. Com base dessas informações responda: Qual a altura do prédio?

Bem, com base dessa relação de proporcionalidade, podemos aplicar o mesmo raciocínio que Tales aplicou quando mediu a altura da pirâmide:

Altura do prédio está para sua sombra, assim como a altura da árvore está para sua sombra:




Faça a regra de três:

1,3x = 2,6 * 10
1,3x = 26

Isole x:

x = 26/1,3
x = 20

Bem, então encontramos a altura do prédio: 20 metros!
Note que a sombra da árvore mede 1,3 metros, justamente a metade da medida de sua altura que é de 2,6 metros! O mesmo ocorre com as medidas do prédio e sua sombra: A medida da sombra do prédio é a metade da medida de sua altura (20/2 = 10).
Portanto, vimos mais uma vez que a proporcionalidade dessa relação é verdadeira.
Mas como Tales demonstrou isso que acabamos de ver?

A demonstração do Teorema de Tales:

Imagine agora três retas paralelas horizontalmente:

Agora imagine que essas três retas foram cortadas por duas transversais:

Em seguida, crie os segmentos formados pela essa intersecção, em cada lado: 

O Teorema de Tales nos afirma que: "Quando duas retas transversais cortam um feixe de retas paralelas, as medidas dos segmentos delimitados nas transversais são proporcionais."

Com essa afirmação podemos dizer o seguinte, à partir do nosso exemplo:

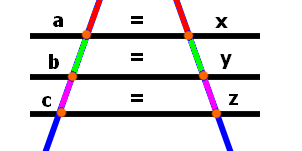
O segmento AB é proporcional ao segmento xy, ou em outras palavras, A está para B, assim como x está para y:



O mesmo ocorre para os segmentos BC e yz:



Veja uma ilustração da situação:

À partir do Teorema de Tales, podemos deduzir que quando há uma proporcionalidade entre dois ou mais elementos, podemos relacioná-los e descobrirmos outras relações proporcionais num mesmo elemento, assim como fizemos para descobrir a altura do prédio no exemplo dessa aula, e como Tales fez para descobrir a altura da pirâmide há mais de 2000 anos atrás.