O que é?
Um método muito eficiente e conhecido na matemática para resolver sistemas lineares, é a utilização da Regra de Cramer.
A regra de Cramer nos diz que:
E assim sucessivamente...
Portanto, com a utilização desta regra, você poderá encontrar os valores de diversas variáveis num sistema linear quadrado, ou seja, o número de variáveis deve ser igual ao número de equações dentro do sistema.
Veremos um exemplo prático:
Utilizando a Regra de Cramer:
Encontre as variáveis do sistema:
O primeiro passo a se fazer para aplicarmos a Regra de Cramer é construir uma Matriz denominada ''D'' contendo apenas os coeficientes das variáveis, na mesma ordem em que elas aparecem no sistema:
Note que a primeira coluna é referente aos coeficientes de ''x'' e os elementos da segunda coluna são referentes aos coeficientes de ''y''.
Agora com a Matriz construída, podemos encontrar seu determinante:
Multiplique os elementos da Matriz principal e subtraia com os elementos do produto da Matriz secundária:
Det (D) = (3*3) - (2*1)
Det (D) = 9 -2
Det (D) = 7
Encontrado o determinante de D, vamos construir a Matriz ''Dx'' onde iremos substituir a coluna dos coeficientes de ''x'' pelos termos independentes do sistema:
Agora iremos encontrar o determinante desta Matriz Dx:
Det (Dx) = 27 - 13
Det (Dx) = 14
Segundo a Regra de Cramer:
Então basta substituir Dx e D na equação, para encontrar x:
Encontrado ''x'' podemos fazer o mesmo para ''y'', criando a Matriz Dy, onde iremos substituir a coluna contendo os coeficientes de y, adicionando em seu lugar os termos independentes do sistema:
Calculando o determinante da Matriz Dy:
Det (Dy) = 39 - 18
Det (Dy) = 21
Encontrado o determinante de ''Dy'', basta substituir na Regra de Cramer:
Então a solução deste sistema é: S=({2; 3)}
Escalonamento de sistemas lineares:
Podemos utilizar o mesmo processo para encontrarmos as variáveis do seguinte sistema:
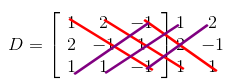
Primeiro crie a Matriz ''D'' apenas contendo os coeficientes das variáveis:
Agora para encontrar o determinante desta Matriz quadrada de ordem 3, utilize a Regra de Sarrus:
Encontrado o determinante da Matriz "Dx'', podemos encontrar o valor de ''x'' substituindo "D" e "Dx" na Regra de Cramer:
Então x =3; Vamos encontrar ''y'':
Construindo a Matriz "Dy" trocando a segunda coluna pelos termos independentes do sistema, iremos ter:
Encontrando seu Determinante:
Det (Dy) = -3 + 2 + (-12) + 4 + (-6) + 3
Det (Dy) = -12
Agora utilize a Regra de Cramer para encontrar o valor de ''y'':
Então y = -4
Por fim, faça o mesmo para a variável ''z''.
Crie a Matriz "Dz'' substituindo sua coluna que contém os coeficientes de ''z'' pelos termos independentes no sistema:
Agora encontre seu determinante:
Det (Dz) = -6 + 6 + 2 + (-24) + (-3) + 2
Det (Dz) = -23
Utilizando Cramer:
Então z = -23/3
Portanto, a solução para este sistema é: S=({3; -4; -23/3})








Resolva as equações usando a fórmula de Bhaskara .
ResponderExcluirA) x²+3x-10= 0
B) x²-5x+4=0
C) x²+8x+12=0
Poderia responder pra mim?
A) delta = 3² - 4 * (-10)
Excluirdelta = 9 + 40
delta = 49
x = -3 mais ou menos V49/2
x' = -3 + 7 /2
x' = 4/2 = 2
x'' = -3 -7/2
x'' = -10 /2 = -5
B) delta = 25 - 4 * 4
delta = 25 - 16
delta = 9
x = 5 mais ou menos V9/2
x' = 5 + 9/2
x' = 14/2 = 7
x''= 5 - 9/2
x'' = -4/2 = -2
C) delta = 8² - 4 * 12
delta = 64 - 48
delta = 16
x = -8 mais ou menos V16/2
x' = -8 + 4/2
x' = -4/2 = -2
x'' = -8 - 4/2
x'' = -12/2 = -6
Vc pode aprender mais sobre equações de segundo grau e fórmula de Bhaskara acessando esse link do blog:
http://aulasmayleone.blogspot.com.br/2014/11/equacoes-do-segundo-grau.html
Bons estudos.
2x-3y=-5
ResponderExcluirx+2y=8 (regra de Cramer)
Pode explicar pfvr...
3x-4y+3z=-1
2x-y-3=-5
x-3y-z=-6