Números Complexos - Introdução

O que é o conjunto dos números complexos?

A matemática pode ser exata na maioria das vezes, mas há casos em que a matemática pode sofrer pequenas divergências.

Um exemplo muito clássico de divergência matemática é a impossível resolução de raízes de índice par com radicando negativo. Algo como: 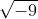 (Raiz quadrada de 9 negativo)

Só relembrando... O que significa mesmo a raiz quadrada de um número ''x''? Significa que algum número elevado ao quadrado resultará em ''x'', certo?

Portanto, temos que: 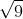 (raiz quadrada de nove) é igual à 3, pois 3 vezes ele mesmo resultará em 9 -> 3*3 ou 3² = 9. E o mesmo ocorre com o -3, onde: (-3)² = (-3) * (-3) = 9, também!

Por fim, dizemos que a raiz quadrada de 9 é igual à 3 positivo e 3 negativo, ou simplesmente mais ou menos 3.

Resolvendo essa pequena equação de 2o grau você pode perceber isso:

x² - 9 = 0

Resolvendo... Basta passar o -9 para o outro lado da igualdade e trocar o seu sinal:

x² = 9

Agora passe o expoente de ''x'' também para o outro lado da igualdade e transforme-o numa raiz quadrada:

Então a solução desta equação seria: S={-3; 3)

E neste caso?

x² + 9 = 0

Faremos então o mesmo procedimento:

Mas o que ocorre quando temos o caso acima?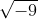 

Que número que elevado à dois resultará em -9? Vou lhe responder... Nenhum! Isso mesmo... Nenhum, por isso que dizemos que raízes com índices pares que contenham radicandos negativos não existem no conjunto dos números reais, pois nenhum número real ao quadrado dará -9.

E então? Ficaremos sem resolução? Não mesmo! Para resolver esse tipo de impasse podemos multiplicar 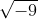 por -1 para trocar o sinal negativo do 9, concorda?

Então:

Pelas regras da radiciação, já que temos uma multiplicação dentro da mesma raiz, podemos separá-las:

Raiz quadrada de 9 tem solução agora (que no caso, seria 3), pois temos 9 positivo dentro da raiz, não 9 negativo como antes, então:

Pois bem, temos agora algo mais exato, porém a raiz quadrada de -1 é impossível de ser resolvida, só podemos fazê-la até aí, e então?

Então nós podemos chamar 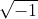 de simplesmente ''i''. ''i'' é uma partícula imaginária e pode facilmente substituir a raiz de menos 1, portanto temos: 

Mas como ''i'' não existe no conjunto dos números reais, devemos estender o nosso conjunto para os números complexos, onde a partícula imaginária, também conhecida como ''i'', existe.

Então a resolução da equação:

Não existe no conjunto dos reais, mas existe no conjunto dos complexos.

Então em resumo, podemos resolver algumas divergências matemáticas (como raízes pares com radicando negativo) utilizando o conjunto dos números complexos, onde neste conjunto a partícula imaginária conhecida por vezes como ''i'' que representa a raiz quadrada de -1, existe.

Definição dos Números Complexos:

Pois bem, agora que você conheceu a partícula imaginária, posso finalmente definir os números complexos.

Mas para que tudo fique mais claro, vamos resolver essa outra equação de segundo grau com os números complexos:

Ao identificar os coeficientes da equação temos que:

a = 1

b = -2

c = 50

Então vamos resolver essa equação através da fórmula de Bháskara e Delta:

Se estivéssemos limitados no conjunto dos números reais, essa equação teria como solução um conjunto vazio, pois não podemos ter delta < 0, ou seja, delta não pode ser um número negativo, mas como estamos trabalhando com o conjunto dos números complexos, essa equação poderá ter solução, veja:

Chegamos então em: 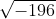, ou seja, uma raiz quadrada negativa!

Para resolver essa raiz com o auxílio dos complexos, vamos multiplicar o -196 por -1 para trocar seu sinal:

Agora podemos separar essa raiz em duas:

Neste momento podemos resolver a raiz quadrada de 196 pois agora se trata de uma raiz positiva:

E então temos 14 multiplicando a raiz de -1:

E como nós podemos chamar a raiz de -1 de ''i'', teremos finalmente:

Então voltando para a equação de segundo grau, iremos obter:

Podemos separar essa fração em duas, contanto que o denominador continue o mesmo:

E dividindo ambas frações por dois, teremos:

E esta é a solução para a equação.

S= {1+7i; 1-7i}

Agora que temos o seguinte resultado:

Irei mostrar a definição dos números complexos, certo?

Temos três possíveis casos de definição, onde:

Onde ''a'' é um número real e ''b'' o coeficiente da partícula imaginária, pois está multiplicando ''i''.

Quando temos algo como Z = a + bi, temos um número complexo, onde temos um número real e um número imaginário.

No caso da nossa resolução da equação: 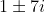, ''1'' é conhecido como parte real, e ''7'' como parte imaginária, pois está multiplicando ''i''.

Quando temos b = 0, não se trata mais de um número complexo, e sim de um número real, pois se ''b'' vale zero e multiplicar ''i'', a partícula imaginária irá sumir da expressão (pois qualquer coisa vezes 0, dará 0) e só restará ''a'' que é um número real:

Z = a + 0*i = Número real

Por fim, quando não temos partes reais na expressão, ou seja, a = 0, e temos apenas partes imaginárias, então temos uma expressão conhecida como ''imaginário puro'':

Z = bi = Imaginário puro

Um exemplo de imaginário puro é a solução desta equação: x² + 9 = 0, que resolvemos no início desta aula e resultou em .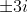

Veja que temos apenas a parte imaginária na resolução da equação, portanto essa solução se trata de um imaginário puro.

Outra coisa a se dizer com relação aos números complexos é o seu conjugado.

Se um número complexo é representado por:

Seu conjugado é representado por:

Ou seja, ao representar o conjugado de um número complexo, nós simplesmente invertemos seu sinal e adicionamos um segmento acima de ''Z'' para deixar expresso que estamos nos referindo ao conjugado de tal número complexo.

Pois bem, este é o final da primeira aula sobre os números complexos! Acompanhe as aulas posteriores para saber mais sobre o assunto.

Bons estudos.