Números Complexos - Potências dos Imaginários

Introdução:

Continuando nosso assunto com relação aos números complexos... Vamos hoje falar sobre as potências dos números imaginários, ou seja, vamos nos atentar às potências de ''i''.

Potências de ''i'':

Observe a seguinte sequência de potências: 

Vamos resolver primeiramente: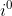 

Sabemos que qualquer número elevado à zero é igual à 1, portanto:

Na sequência temos: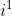 

Mas ''i'' elevado à 1 só pode ser ele mesmo, não concorda?

Próximo da sequência...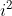 

Quanto vale ''i'' mesmo? Não se lembra? Na aula passada fora mencionado que ''i'' é o mesmo que raiz quadrada de menos 1: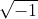 

Então temos que i² = 

Cancelando o expoente de -1 com o índice da raiz quadrada ficamos com:

i² = -1

Por fim temos que resolver: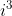 

Teremos então: i² * i, e sabendo que i² vale -1 e que ''i'' vale o próprio ''i'', tenha:

i² * i  -> (-1)i ou simplesmente -i.

Então a sequência fica da seguinte forma:

Vamos agora resolver a próxima sequência:

Veja a resolução de cada potência ao lado da mesma:

A sequência então fica assim:

Note que a sequência se repete, pois anteriormente tínhamos os mesmos resultados ordenados da mesma maneira, porém com expoentes diferentes, veja:

E você já deve ter percebido que com a próxima sequência o mesmo irá ocorrer, ou seja:

O que podemos concluir aqui? Que a sequência de resultados (1, i, -1, -i) se repete de quatro em quatro vezes.

Então para descobrirmos por exemplo, quanto vale: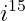 

Basta dividirmos o expoente do número imaginário por 4:

Mas na realidade o que nos interessa nessa divisão é seu resto, ou seja, neste caso, o 3.

Por fim, basta substituir o expoente do número imaginário pelo resto da divisão: i³

E como você já viu... i³ é igual à -i, portanto:

Vamos conferir?

Nós tínhamos a seguinte sequência:

Então continuando de onde paramos...

E aí está exatamente o resultado de i elevado na décima quinta, portanto, está confirmada a eficácia deste método.

Vamos então descobrir o valor de: 

Na realidade, para dividir um número qualquer por 4 e obter seu resto, não há a necessidade de dividir o número todo, você pode simplesmente dividir apenas as duas últimas unidades que funciona da mesma forma, veja:

Viu? Ambas divisões nos resultou no resto igual à dois.

Substituindo o expoente do imaginário pelo resto da divisão:

Onde i² na realidade vale -1, teremos finalmente:

Operações com as potências de ''i'':

Agora que você sabe como calcular todas as potências da partícula imaginária, que tal calcular essa expressão de números complexos contendo potências de ''i''?

Vamos primeiramente descobrir os valores das potências das partículas imaginárias antes de qualquer coisa, ou seja:

Vamos resolver primeiramente: 

Dividindo o expoente por 4, teremos:

Então temos que:

O próximo seria 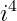 mas vimos mais acima que i elevado à quatro equivale à ''1'', então:

Vamos então calcular o próximo: 

Divisão por 4:

Ou seja:

E por fim iremos calcular: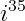 

Realizando a divisão:

Portanto:

Então temos as seguintes resoluções:

Basta então trocar esses valores na expressão:

E por fim simplesmente reduza os termos comuns:

Resultado da expressão:

Pois então, aqui se encerra a segunda aula sobre os números complexos. Acompanhe as aulas posteriores para continuar estudando. Até a próxima.

0