Introdução:
Para desenvolver uma expressão do tipo: (a+b)² basta aplicar a propriedade distributiva:
(a+b) (a+b)
Onde “a” irá multiplicar todos os termos do segundo
parênteses, primeiramente:
a * a = a²
a * b = ab
E desenvolvendo “b”, ele irá multiplicar também todos os termos do
segundo parênteses:
b * a = ab
b * b = b²
Então ao desenvolver por fim a expressão, você terá:
a² + ab + ab + b²
E somando os termos semelhantes ‘’ab’’ fique com 2ab, ou
seja:
a² + 2ab + b²
Veja nossa expressão (a+b)² desenvolvida com o método da propriedade distributiva:
a² + 2ab + b²
Note que a expressão possui 3 termos: ''a²'', ''2ab'' e ''b²''.
Um fator curioso a ser ressaltado nesta aula é o seguinte: O número de termos da expressão do tipo 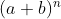 , será igual ao expoente da expressão + 1.
, será igual ao expoente da expressão + 1.
Como assim?
A expressão: (a+b)² possui como bem observado, 3 termos, e seu expoente é o dois. Então com base nesta análise, podemos dizer que a quantidade de termos desta expressão é igual ao valor de seu expoente somando 1, ou seja: 2 + 1 = 3.
Isso significa que, sem realizar qualquer tipo de cálculo, podemos afirmar que a expressão (a+b)³ possui quatro termos ou seja, seu expoente que é 3 somado com 1, que dará quatro. Assim como a expressão  possui 5 termos. Soma-se seu expoente com 1 e encontra-se a sua quantidade de termos corretamente.
possui 5 termos. Soma-se seu expoente com 1 e encontra-se a sua quantidade de termos corretamente.
Por tanto, essa ideia vale para qualquer expressão do tipo: 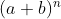
Mas voltando ao início... No caso de desenvolver a expressão (a+b)², algo similar poderia ter sido realizado por meio dos ‘’produtos notáveis’’.
Para desenvolver uma expressão do tipo: (a+b)³ ambos processos apresentados acima nos resultaria no desenvolvimento correto da expressão, mas por vezes estes métodos podem ser trabalhosos e cansativos de serem realizados quando temos um expoente muito grande, como por exemplo a expressão: 
Desenvolver esta expressão por meio dos produtos notáveis ou através da propriedade distributiva não é impossível, porém, como já dito, é muito trabalhoso. Por isso, o estudo do método do Binômio de Newton e o Triângulo de Pascal são muito importantes para sabermos como resolver expressões como essas do tipo: 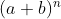
A fórmula:
Indo direto ao ponto e sem teorias, a fórmula para o termo
geral do Binômio de Newton é a seguinte:
Com o auxílio desta fórmula, você pode encontrar algum termo específico na expressão, ou o coeficiente e o termo independente de determinado número dentro da expressão.
Vamos por partes... O que cada letra significa na fórmula?
Na expressão do tipo: 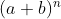 podemos dizer que na fórmula, ''a'' e ''b'' correspondem aos termos da expressão, isso é um tanto quando óbvio e ''n'' é o expoente da mesma.
podemos dizer que na fórmula, ''a'' e ''b'' correspondem aos termos da expressão, isso é um tanto quando óbvio e ''n'' é o expoente da mesma.
''T''significa termo. Então quando queremos encontrar um determinado termo na expressão, substituímos-o por ''p'' na fórmula. Mas analisando a fórmula em si, note que ''p'' aparece somando o 1. Então logicamente se queremos encontrar o terceiro termo da expressão, ''p'' não pode ser 3, porque 3+1 = 4. Então daí estaríamos calculando o quarto termo da expressão e não o terceiro como desejamos. Por isso, ''p'' sempre será o antecessor ao número do termo que queremos encontrar, ou seja, se desejamos encontrar o terceiro termo da expressão, ''p'' será seu antecessor, ou seja, 2, pois: 2+1 = 3.
Então sabendo quais são os valores que devemos substituir corretamente na fórmula, vamos ver um exemplo prático?
Vamos primeiramente tirar a prova da eficácia desta fórmula, encontrando um termo de uma expressão já desenvolvida. No caso, vamos encontrar, por exemplo, o terceiro termo na expressão (a+b)²
Então na fórmula teremos que substituir os seguintes valores:
n = 2 (expoente da expressão)
p = 2 (pois queremos encontrar o terceiro termo da expressão, porém ''p'' sempre será o antecessor deste número, ou seja, 2)
Então ficamos com:
E resolvendo:
2+ 1 = 3
Então:
Agora aqui: 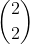 temos uma combinação do tipo ''combinação dois à dois''. Em combinação, quando temos o mesmo número em cima e em baixo, seu resultado será 1, ou seja:
temos uma combinação do tipo ''combinação dois à dois''. Em combinação, quando temos o mesmo número em cima e em baixo, seu resultado será 1, ou seja:
Resolvendo o expoente de ''a'' temos 2-2, que resultará em zero. E sabe-se que qualquer número elevado à zero é igual à 1, portanto:
E 1 vezes b² é o próprio b².
Por fim temos que:
Ou seja, o terceiro termo da expressão (a+b)² é b². E de fato:
a² + 2ab + b²
Pois bem, vamos ver agora a mesma expressão, porém com o segundo termo?
Os valores a serem substituídos na fórmula são:
n = 2
p = 1
Logo:
Então:
E na combinação:  , quando temos o número de baixo igual à 1, seu resultado será o número de cima, portanto:
, quando temos o número de baixo igual à 1, seu resultado será o número de cima, portanto:
Resolvendo o expoente de ''a'', temos 2-1 = 1, portanto:
Não precisamos escrever o ''1'' nos expoentes se não quisermos:
Concluindo... Temos o 2 multiplicando a que multiplica b, portanto:
Isso quer dizer que, o segundo termo da expressão (a+b)² é 2ab, o que não é mentira:
a² + 2ab + b²
Com base do que foi passado, podemos então descobrir algum dos termos da seguinte expressão:
Para este exemplo, podemos encontrar o quinto termo da expressão, o que acha?
Então teremos o seguinte:
a = x
b = 4
n = 8
p = 4
Então com os valores substituídos na fórmula, teremos algo como isto:
Ou então:
Agora temos a seguinte combinação: 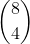
(Leia a aula sobre combinações para saber como resolvê-las)
Realizando a combinação, teremos:
Então ao resolver a combinação, teremos:
Agora resolvendo o expoente de ''x'': 8-4 é 4, portanto:
4 elevado à 4 é igual à 256, então:
E por fim, multiplicando 70 por 256, teremos o quinto termo da expressão 
Vamos ver mais um exemplo?
Na expressão:
A fórmula:
Valores a serem substituídos:
a = y²
b = 3
n = 4
p = 3
Então teremos:
E também:
Resolvendo a combinação:
A equação fica assim:
Resolvendo o expoente de "y²'' 4-3 = 1, então multiplicando o expoente de y que é dois, com 1, obtenha o próprio 2:
3 ao cubo é 27:
E 27 vezes 4 é 108, portanto o quarto termo da expressão




Muito Obrigado Mayara Leone, você realmente me ajudou muito!! Estive caçando essa matéria pela internet, e ate assisti a alguns videos mas não conseguir entender, mas com essa sua explicação conseguir realmente entender. Muito Obrigado foi um excelente trabalho.
ResponderExcluir