Olá! Na resolução sobre física de hoje, teremos a seguinte questão que caiu na UERJ do Rio de Janeiro:
Um bloco de massa igual a 1,0 kg repousa em equilíbrio sobre um plano inclinado. Esse plano inclinado tem um comprimento igual a 50 cm e alcança uma altura máxima em relação ao solo igual a 30 cm. Calcule o coeficiente de atrito entre o bloco e o plano inclinado.
Então vamos lá pessoal... Vamos imaginar primeiro o plano inclinado... Ele tem um comprimento de 50 cm, como dito no problema, e como ele é inclinado ele segue essa forma:
Lembrando que aquele segmento em marrom na ilustração é o solo, e o comprimento do mesmo com relação ao plano inclinado é desconhecido.
Bem, não podemos nos esquecer de que esse plano inclinado tem uma altura de 30 cm com relação ao solo:
É fácil observar que temos aqui um triângulo retângulo por conta da presença do ângulo reto de 90 graus entre os catetos, e também uma angulação formada entre o solo e o plano inclinado, onde chamaremos de ângulo teta (θ).
O bloco está em repouso sobre o plano inclinado:
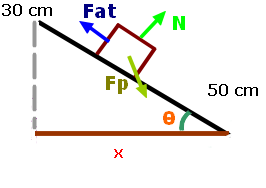
Agora vejamos as forças que atuam sobre o bloco... Se ele está em repouso isso indica que ele está parado, logo, não há aceleração, porém há a força de atrito contrária à direção de inclinação do bloco, mais conhecida como (Fat):
Temos também a força normal que não deixa o bloco afundar:
E por fim, a força Peso (Massa vezes aceleração da gravidade):
Por conta da inclinação do vetor da força peso (Fp) podemos decompor este vetor e obter seus componentes: Fx (Força x apontada para a direção de inclinação do bloco) e Fy (Força y perpendicular à Normal):
Se este bloco se encontra em equilíbrio, o mesmo tem como força resultante 0:
Fr = 0
As forças que atuam sobre o bloco são: Fat, N, Fy e Fx.
Como a força normal (N) e a força Y (Fy) tem o mesmo módulo e são perpendiculares com seus vetores em sentidos opostos, uma anula a outra.
Portanto temos que:
Fr = Fx - Fat = 0
Isso porque a força x tem o vetor no sentido oposto à força de atrito (Fat) então a força resultante (Fr) será uma subtração entre uma e outra.
Isolando ''Fx'', passando "Fat'' para o outro lado da igualdade temos que:
Fx = Fat
Sabemos que:
Fx = P*Sen(θ)
Onde "P'' é a força peso, ou seja, massa vezes aceleração da gravidade.
Sabemos também que:
Fat = μ*N
Onde " μ" é o coeficiente de atrito (o que é pedido no problema) e "N" é a força normal.
Se a força normal é igual à força Y (como visto mais acima) sabemos que:
Fy = P*Cos(θ)
Logo, a força normal (N) é igual à: P*cos(θ)
Ou seja, a força de atrito (fat) pode ser escrita da seguinte forma:
Fat = μ. P*cos(θ)
Lembrando que: Fx = Fat
Então por lógica... Se:
Fx = P*Sen(θ)
E
Fat = μ. P*cos(θ)
De acordo com a relação: Fx = Fat temos o seguinte:
P*Sen(θ) = μ. P*cos(θ)
Anulando "P" dos dois lados da igualdade, teremos:
Sen(θ) = μ.*cos(θ)
Como o coeficiente de atrito ( μ) é o que queremos achar, podemos isolá-lo na equação passando o cosseno de teta para o outro lado da igualdade que está multiplicando, dividindo:
Lembrando das relações trigonométricas...
Podemos perceber que a razão entre o seno de um ângulo com o cosseno desse mesmo ângulo nos resultará na tangente do ângulo citado:
Ou seja, o coeficiente de atrito entre o bloco e o plano inclinado será igual à tangente do ângulo teta do triângulo retângulo.
A tangente em trigonometria pode se relacionar entre o cateto oposto e o cateto adjacente do ângulo referido (no caso aqui, o ângulo teta):
Relacionado ao ângulo teta, o cateto adjacente é o lado que mede 'x' e o cateto oposto é o lado que mede 30 cm, tendo também sua hipotenusa igual à 50 cm.
Se a tangente relaciona cateto oposto por cateto adjacente, devemos relacionar 30 cm com x, assim:
Como não sabemos o valor do cateto adjacente, podemos utilizar o Teorema de Pitágoras para descobrir seu valor:
h² = a² + b²
Se ''h'' é a hipotenusa e ''a'' e ''b'' seus respectivos lados, logo:
50² = 30² + x²
2500 = 900 + x²
2500 -900 = x²
1600 = x²
√1600 = x
40 = x
Então com relação ao do ângulo teta, o cateto adjacente mede 40 cm:
Se: 
Isso indica que 
Logo, o coeficiente de atrito entre este bloco e este plano inclinado é 0,75.
Outro método alternativo para resolver esta questão considerando a massa do bloco é o seguinte:
Massa do bloco = 1 kg
Logo, seu peso será igual à sua massa vezes a aceleração da gravidade, comumente dita como 10 m/s², então
P = 1*10 = 10N
Se sabemos que:
Fx = P*Sen(θ) E ''P'' vale 10, então:
Fx = 10*Sen(θ)
A ''Fat'' valerá:
Fat = μ*P*cos(θ)
Se "P" vale 10, logo ''Fat'' vale:
Fat = μ*10*cos(θ)
A relação nos diz que: Fx = Fat, então:
10*Sen(θ) = μ*10*cos(θ)
Anulando ''10'' de ambos lados da igualdade, teremos novamente:
Sen(θ) = μ*cos(θ)
E o exercício segue como anteriormente à partir daí, pois o coeficiente de atrito não depende da força peso para ser encontrado.











0 comentários:
Postar um comentário