O Teorema de Pitágoras

O que é?
O Teorema de Pitágoras é uma relação métrica que relaciona os lados dos triângulos retângulos.
Um triângulo retângulo é conhecido por conter um ângulo reto internamente:

Para um triângulo retângulo é fácil afirmar que o lado oposto ao ângulo reto será sempre o lado chamado de ''Hipotenusa'', que por sua vez, também seria o maior lado do triângulo.
Para os outros lados (a base e a altura do triângulo retângulo) temos os chamados catetos.

Vamos nomear nosso triângulo retângulo de'' triângulo ABC'', onde ''A'' é a Hipotenusa e ''B'' e ''C'' são os catetos:

Note que o lado ''A'' (a hipotenusa) está sempre oposta ao ângulo reto de 90 graus:

O Teorema de Pitágoras afirma que em qualquer triângulo retângulo, o quadrado da Hipotenusa será sempre igual à soma dos quadrados dos catetos.
Se temos ainda o triângulo ABC, podemos afirmar à partir do Teorema de Pitágoras, a seguinte relação:

a² = b² + c²

Lembrando que ''A'' refere-se à Hipotenusa, e ''B'' e ''C'' aos lados do triângulo retângulo.

A demonstração do Teorema de uma forma resumida:

Pitágoras demonstrou sua relação métrica entre os lados dos triângulos retângulos da seguinte maneira:

Onde ele afirma que o quadrado em verde possui a área igual à soma das outras duas áreas dos outros dois quadrados.
Considerando que o quadrado verde se refere à hipotenusa do triângulo retângulo formado pelos três quadrados, os outros dois quadrados, o azul e o rosa, são os catetos do mesmo.
Por isso podemos concluir que elevamos os lados do triângulo retângulo ao quadrado no Teorema de Pitágoras, porque ele relacionou a área desses quadrados para determinar essa relação métrica, e a unidade de medida de área é sempre elevada ao quadrado.
O Tereoma de Pitágoras foi muito útil para o desenvolvimento da trigonometria e de outras relações geométricas (e até mesmo algébricas).

Veja uma demonstração sobre a verdade do Teorema:
Considere um triângulo retângulo de catetos 4 e 3, e hipotenusa igual à 5:

Utilizando o Teorema de Pitágoras, podemos afirmar que: ''O quadrado da hipotenusa é igual à soma dos quadrados dos catetos''.
Nesse caso, a hipotenusa é 5, e os catetos são 4 e 3, logo:

a² = b² + c²
5² = 4² + 3²
25 = 16 + 9
25 = 25

A equação foi satisfeita, logo podemos afirmar que o Teorema de Pitágoras é correto.

Sabendo disso, podemos  encontrar o lado de um triângulo retângulo, sabendo apenas dois de seus lados à partir do Teorema de Pitágoras, vamos ver?

Num triângulo retângulo com catetos iguais à 6cm e 8cm, encontre a Hipotenusa.

Podemos utilizar o Teorema de Pitágoras para encontrarmos a hipotenusa, veja:

a² = b² + c²
Podemos substituir ''b'' e ''c'' no Teorema, pelas medidas dos lados fornecidos, não importando quem seja ''b'' ou ''c'':

a² = 6² + 8²
a² = 36 + 64
a² = 100
Resolvendo essa equação de 2º grau incompleta temos:

a = √100
a = 10

Logo, a hipotenusa desse triângulo retângulo mede 10 cm.
Vamos conferir?
Substitua esses valores no Teorema:

10² = 6² + 8²
100 = 36 + 64
100 = 100

Confere!
Vamos ver mais um exemplo?

A hipotenusa de um triângulo retângulo mede 20 cm, e um dos catetos possui 16 cm. Encontre a medida do outro cateto.

Aplicando Pitágoras, temos:

20² = 16² + c²
400 = 256 + c²
Agora isole ''c²'' na equação:
400 - 236 = c²
144 = c²
Resolvendo a equação do 2º grau incompleta:
√144 = c
12 = c

Então o outro cateto mede 12 cm, vamos conferir?

20² = 16² + 12²
400 = 256 + 144
400 = 400

Novamente confere! Tudo certo!

Veja mais outro exemplo:

Encontre a medida do terceiro lado do triângulo retângulo abaixo:

Note que na imagem, a hipotenusa é o lado que mede 7 m por estar oposta ao ângulo reto, logo o lado que queremos encontrar é o segundo cateto, visto que um deles já é conhecido e mede 6 m.

a² = b² + c²
7² = 6² + x²
49 = 36 + x²
49 - 36 = x²
13 = x²
√13 = x²
√13 é aproximadamente 3,6

Então o terceiro lado desse triângulo mede aproximadamente 3,6 metros.
Conferindo:

49 = 36 + 3,6²
49 = 36 + 12,96
49 = 48,96 (aproximadamente 49, confere!)

Agora preste atenção no problema abaixo:

Um rapaz deseja sair da cidade ''A'' e tem como destino a cidade ''C''.
A cidade A se encontra verticalmente posicionada à uma cidade B e a distância entre essas duas cidades é de 50 km. Essa distância (AB) é perpendicular à distância entre as cidades B e C. A distância entre as cidades B e C é de 30 km. Porém, o rapaz pensa que viajar da cidade A até a cidade C diretamente fosse mais vantajoso à ele.
Ele está correto em afirmar isso? Qual é a distância entre as cidades A e C?

Bem, vamos começar a montar nossa situação de acordo com o que foi pedido no enunciado:

Nós temos três cidades, uma delas é a cidade A que é onde o jovem se encontra. 
Depois temos ainda a cidade B, onde a distância entre essas duas cidades é de 50 km.
Nosso desenho então fica assim:

Eu sei que essa reta que liga os pontos A e B é vertical, porque o problema me informou isso.
A distância AB como bem informada pelo problema, é perpendicular à distância BC, ou seja, forma-se um ângulo reto de 90 graus entre essas duas retas.
Lembrando que essa distância (BC) tem 30 km, logo:

Veja que o problema nos pede para encontrarmos a distância AC (entre a cidade A e a cidade C), então podemos ligar essas duas cidades com um segmento de reta da seguinte forma:

Então aí está nosso triângulo retângulo! 
Vamos agora encontrar o terceiro lado desse triângulo, que seria justamente a distância entre as cidades A e C.

Relacionado ao ângulo reto de 90 graus, podemos facilmente visualizar que a distância AC (x) é a hipotenusa, sendo assim, as distâncias AB e BC são nossos catetos.
Utilizaremos o Teorema de Pitágoras para solucionarmos este problema:

a² = b² + c²
x² = 50² + 30²
x² = 2500 + 900
x² = 3400
x = √3400
x = aproximadamente 58,3 km.

Então a distância entre a cidade A e a cidade C tem um pouco mais de 58 km. Mas não paramos por aí... O problema nos pergunta se o rapaz estava correto em afirmar que percorrer essa distância diretamente sem passar pela cidade B seria mais vantajoso.

Veja: Da cidade A até a cidade C ele percorreria um pouco mais que 58 quilômetros. Se ele quisesse optar por passar pela cidade B, e da cidade B partir para a cidade C ele iria percorrer:
Da cidade A (onde ele está) até a cidade B, ele percorrerá 50 km, mais 30 km da cidade B até a cidade C, ou seja: 50 + 30 = 80 km.
Logo, ele está correto em afirmar que percorrer da cidade A até a cidade C seria mais vantajoso à ele, já que ele só iria percorrer 58 km, passando pela cidade B e depois indo para a cidade C, ele iria percorrer um total de 80 km, ou seja, ele ganharia um pouco mais de 21 km de vantagem se percorrer da cidade A até a cidade C, diretamente. 

Agora veremos um exemplo diferente...
É muito comum encontrar em provas e testes o seguinte:

Para se calcular a área de um triângulo qualquer, podemos multiplicar o valor de sua base pela sua altura, e depois dividir esse resultado por dois. 
Considerando o triângulo equilátero abaixo, calcule sua área:

Certo, nós aprendemos até aqui a calcular catetos e hipotenusas de triângulos retângulos, mas o que temos aqui é um triângulo equilátero (todos os lados são iguais) medindo 8 cm cada lado.
Mas podemos calcular a área de um triângulo qualquer (incluindo os equiláteros) utilizando o cálculo da multiplicação entre a altura do triângulo pela sua base, e dividindo esse resultado por dois, segundo o enunciado do problema.
Perceba que temos apenas a informação dos lados do triângulo (8 cm cada) e como trata-se de um triângulo equilátero, podemos concluir que sua base também mede 8 cm. Certo, a base já sabemos... Mas e a altura?
Note que se traçarmos uma reta que corta esse triângulo no meio:

Ela será justamente a altura do triângulo! Que beleza, ein? Mas como saber a medida dessa altura?
Matemática não é só decorar fórmulas e realizar cálculos, você precisa ter visão sobre as coisas... Então analise esse triângulo e tire suas próprias conclusões.
Como podemos encontrar a altura deste triângulo? Será que o Teorema de Pitágoras pode nos auxiliar nesta tarefa?
Sim, ele pode! Acompanhe o raciocínio que tudo se esclarecerá:

Perceba que criando essa linha que corta o triângulo no meio, nós iremos obter dois triângulos retângulos, um de cada lado.
Lembre-se que a base do triângulo interiço media 8 cm, mas ao cortarmos ele ao meio, dividimos então seu valor pela metade, ou seja: 8/2 = 4. Logo, a base dos triângulos retângulos possuem 4 cm cada.

Depois de tudo isso... Se você chegou até aqui e entendeu o desenrolar da estória... Não acha que o que vem agora não é óbvio?
Analise a situação: Queremos encontrar a altura do triângulo, essa altura será justamente a medida desse segmento de reta traçado bem ao meio do triângulo equilátero.
Note a imagem... Temos dois triângulos retângulos formados por este segmento de reta, a altura do triângulo. Porém, vamos trabalhar apenas com um dos triângulos retângulos (não importa qual). Veja que o lado que mede 4 cm se refere à um dos catetos, e o lado medindo 8 cm se refere à hipotenusa! Você concorda que o outro cateto (h) não é exatamente a altura que procuramos?
Como o Teorema de Pitágoras pode nos ajudar nessa situação?
Simples! Utilizando o Teorema de Pitágoras, podemos identificar o outro cateto do triângulo retângulo, ou seja, sua altura, veja:

a² = b² + c²
Se a = hipotenusa, b e c = catetos; então:

8² = 4² + h²
64 = 16 + h²
64 - 16 = h²
48 = h²
√48 = h
h = aproximadamente 6,9. (Ou arredondando, h = 7)

Então a altura desse triângulo equilátero com lados medindo 8 cm é de 6,9 ou 7 cm.
Mas não é isso que o problema nos pede... Ele quer a área do triângulo. Lembra como fazer?

Multiplique a base do triângulo (vamos chamar de ''b'') pela altura (h) e dividir isso tudo por dois.
Esse cálculo nos resulta na seguinte fórmula:



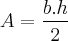
Basta agora substituir os valores:

A base, como já dito, mede 8 cm por se tratar de um triângulo equilátero.
Não se confunda: Aqueles 4 cm eram dos triângulos retângulos, mas para aplicarmos a medida da base na fórmula, o correto é aplicar o valor da base do triângulo inteiro, que é o que queremos encontrar, se não iríamos encontrar a área de apenas um dos triângulos retângulos.
Certo, a base já sabemos... A altura também, acabamos de calcular: h = 6,9
Vamos jogar esses valores na fórmula?



Então a área total desse triângulo equilátero é igual à 27,6 cm².

Finalização:
Como pode ver depois de tantos exemplos, o Teorema de Pitágoras foi e ainda é muito útil para o ramo trigonométrico e matemático, mas ele possui suas limitações! Por exemplo: O que fazer quando nós queremos encontrar dois lados do triângulo e obviamente só temos a informação de um deles?
Há um modo mais ''complexo'' de se resolver esse tipo de dúvida, mas há caminhos mais fáceis! Por que não experimenta dar uma lida na próxima aula sobre o assunto, para tirar essa dúvida?

Próxima aula: Trigonometria do Triângulo Retângulo -> Clique aqui.

Bons estudos.