O que é?
Quando temos uma igualdade entre logaritmos, variáveis ou números reais, temos consequentemente uma equação logarítmica.
Um exemplo muito simples de uma equação logarítmica é este aqui:
Tipo 1 de equações logarítmicas:
Neste exemplo, temos uma equação logarítmica onde há uma igualdade entre um logaritmo e uma incógnita.
Para resolver esse tipo de equação, aplicamos a definição dos logaritmos vista na aula 1 sobre o assunto, então:
Resolvendo primeiramente log de 125 na base 5, temos:
A equação então fica:
Aqui você pode aplicar a propriedade da potência, e passar aquele 3 no denominador para o numerador e fazer com que seu expoente fique negativo, então:
Cancelando as bases iguais:
E multiplicando os dois membros da equação por (-1) tenha:
Portanto a solução para esta equação é: S={-3}
Outro exemplo mais simples ainda deste tipo de equação é o seguinte:
Aqui nós temos uma igualdade entre um logaritmo e um número real.
Primeiramente vamos nos recordar das Condições de Existência dos logaritmos, onde o logaritmando deve ser maior que zero.
Portanto:
x² - 1 > 0
Para resolver uma equação deste tipo, basta novamente aplicar a definição dos logaritmos:
E passando aquele 3¹ (que na verdade é apenas 3) para o outro lado da igualdade:
Somando os termos semelhantes:
Portanto temos uma equação de segundo grau incompleta, onde b = 0.
Para resolver essa equação, basta passar o termo independente para o outro lado da igualdade:
E o expoente de ''x'' ao passar para o outro lado da igualdade, torna-se uma raiz quadrada:
Portanto:
Ou seja, nossas raízes da equação são: -2 e 2.
Mas antes de criar o conjunto da solução, precisamos ''testar'' nossas duas raízes na condição de existência dessa equação, que seria:
x² - 1 > 0
Testando -2, primeiramente:
(-2)² - 1 > 0
4 - 1 > 0
3 > 0
3 é maior que zero, portanto a raiz ''-2'' serve para a equação.
Testando a raiz ''2'' agora:
2² - 1 > 0
4 - 1 > 0
3 > 0
Inequação verdadeira! Então as raízes -2 e 2 servem para a equação:
S={-2; 2}
Veja outro exemplo deste tipo de equação:
Neste exemplo temos uma igualdade entre um número real e logaritmos de mesma base.
Novamente temos uma incógnita no logaritmando, portanto devemos aplicar a C.E (Condição de existência) para o logaritmando, onde:
x + 2 > 0
E também:
x - 2 > 0
Vamos resolver a equação aplicando a definição: Como não temos a base escrita, então tratam-se de logaritmos decimais, então:
Então resolvendo a equação temos:
Portanto a raiz da equação é 5.
Vamos testá-la na C.E?
x + 2 > 0
5 + 2 > 0
7 > 0
E testando também em:
x - 2 > 0
5 - 2 > 0
3 > 0
Tudo correto, portanto a solução desta equação é 5:
S = {5}
Outro exemplo desse tipo de equação:
Novamente temos uma igualdade entre logaritmos de mesma base e um número real.
Aplicando a C.E do logaritmando:
x - 3 > 0
E resolvendo a equação através da definição:
Portanto a raiz da equação é 7.
Vamos verificar se 7 se aplica a condição de existência:
x - 3 > 0
7 - 3 > 0
4 > 0
Tudo correto!!
Veremos mais este outro exemplo um pouco mais ''complexo'':
Essa equação caiu na PUC do Rio Grande do Sul e trata-se de uma igualdade entre um número real e um logaritmo onde temos uma incógnita na base e no logaritmando.
A C.E aplica-se ao logaritmando, onde:
10 + 3x > 0
E para a base, onde a mesma deve ser de positiva e diferente 1:
x ≠ 1
x > 0
Resolvendo essa equação pela definição:
Re-organizando a equação de 2o grau:
Encontrando as raízes reais:
Então temos duas raízes para a equação: 5 e -2.
Testando o 5 na C.E para o logaritmando, temos:
10 + 3x > 0
10 + 3*5 > 0
10 + 15 > 0
25 > 0
E agora testando o -2:
10 + 3(-2) > 0
10 - 6 > 0
4 > 0
5 e -2 servem para o logaritmando, mas ambas raízes devem servir também para a base:
x ≠ 1
x > 0
Testando o 5 primeiro:
5 ≠ 1
5 > 0
Certo! E quanto ao -2?
-2 ≠ 1 Até aqui tudo bem, porém:
-2 > 0 Essa inequação é falsa, pois -2 é menor que zero. Portanto a raiz ''-2'', apesar de servir no logaritmando, não serve para a base.
Então concluímos que a solução é apenas 5: S={5}
Tipo 2 de equações logarítmicas:
Outro Exemplo mais simples de equações logarítmicas que você poderá se deparar, são aquelas equações onde temos uma igualdade entre logaritmos de mesma base, por exemplo:
A C.E para o logaritmando deve ser:
2x + 4 > 0
e
3x + 1 > 0
Em casos como este, para solucionar uma equação logarítmica deste tipo, ou seja, uma igualdade entre logaritmos de mesma base, basta ''esquecer'' a base e resolver apenas a equação, assim:
2x + 4 = 3x + 1
2x - 3x = 1 - 4
- x = -3
x = 3
E verificando na condição de existência essa raiz:
2x + 4 > 0
2*3 + 4 > 0
6 + 4 > 0
10 > 0
E também:
3x + 1 > 0
3*3 + 1 > 0
9 + 1 > 0
10 > 0
Inequações verdadeiras, portanto: S={3}
Agora iremos resolver:

C.E:
3x + 2 > 0
e
2x + 5 > 0
Ignorando as bases iguais, teremos a equação:
3x + 2 = 2x + 5
Resolvendo:
3x - 2x = 5 - 2
x = 3
Verificando a raiz na condição de existência:
3x + 2 > 0
(3*3) + 2 > 0
9 + 2 > 0
11 > 0
e
2x + 5 > 0
(2*3) + 5 > 0
6 + 5 > 0
11 > 0
Inequações verdadeiras.
Agora iremos resolver:
C.E:
3x + 2 > 0
e
2x + 5 > 0
Ignorando as bases iguais, teremos a equação:
3x + 2 = 2x + 5
Resolvendo:
3x - 2x = 5 - 2
x = 3
Verificando a raiz na condição de existência:
3x + 2 > 0
(3*3) + 2 > 0
9 + 2 > 0
11 > 0
e
2x + 5 > 0
(2*3) + 5 > 0
6 + 5 > 0
11 > 0
Inequações verdadeiras.
Tipo 3 de equações logarítmicas:
Por último, o terceiro tipo de equação logarítmica que você poderá encontrar é o seguinte: Equações que devemos utilizar as propriedades dos logaritmos!
Por exemplo, simplifique essa equação genérica:

Perceba que podemos aplicar inversamente as propriedades dos logaritmos, nas condições abaixo:

Em vermelho, podemos aplicar a propriedade da potência, em verde a propriedade do produto e em azul a propriedade do quociente, já que todos os logs estão na mesma base 5.
Fazendo um de cada, teremos assim:
Propriedade do produto:
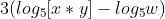
Propriedade do quociente:
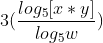
Propriedade da potência:
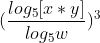
E aí está!
Agora que sabe que pode aplicar as propriedades dos logaritmos nas equações (de acordo com suas necessidades) resolva a seguinte equação:

Primeiramente lembre-se da C.E para o logaritmando:
x + 8 > 0
e
x - 6 > 0
Agora vamos resolver a equação.
Percebeu que temos uma subtração de logaritmos de mesma base? Pois então, podemos simplificar essa equação e transformá-la numa divisão de logaritmos de mesma base:

Agora que temos uma igualdade entre um logaritmo e um número real, podemos aplicar a definição de logaritmos, pois agora temos o caso de equação do tipo 1:

E finalmente:

Agora você pode se livrar do denominador da fração que está dividindo, passando para o outro lado da igualdade multiplicando, então:

Aplicando a propriedade distributiva:

Resolvendo a equação de primeiro grau:

Então se ''x'' é 8, vamos testá-lo na condição de existência:
C.E:
8 + 8 > 0
e
8 - 6 > 0
Inequações verdadeiras, portanto a solução da equação é: S={8}
Verifique na equação para se certificar se está correto, substitua ''x'' por 8 e veja:

8+8 = 16 e 8-6 = 2, então temos:
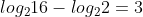
Log de 16 na base 2 é 4 e log de 2 na base 2 é 1, então:

Equação verdadeira.
E temos também os casos que devemos aplicar a quarta propriedade logarítmica, e isso quando temos uma igualdade entre logaritmos de bases diferentes e um número real (ou uma incógnita), por exemplo:
Por exemplo, simplifique essa equação genérica:
Perceba que podemos aplicar inversamente as propriedades dos logaritmos, nas condições abaixo:
Em vermelho, podemos aplicar a propriedade da potência, em verde a propriedade do produto e em azul a propriedade do quociente, já que todos os logs estão na mesma base 5.
Fazendo um de cada, teremos assim:
Propriedade do produto:
Propriedade do quociente:
Propriedade da potência:
E aí está!
Agora que sabe que pode aplicar as propriedades dos logaritmos nas equações (de acordo com suas necessidades) resolva a seguinte equação:
Primeiramente lembre-se da C.E para o logaritmando:
x + 8 > 0
e
x - 6 > 0
Agora vamos resolver a equação.
Percebeu que temos uma subtração de logaritmos de mesma base? Pois então, podemos simplificar essa equação e transformá-la numa divisão de logaritmos de mesma base:
Agora que temos uma igualdade entre um logaritmo e um número real, podemos aplicar a definição de logaritmos, pois agora temos o caso de equação do tipo 1:
E finalmente:
Agora você pode se livrar do denominador da fração que está dividindo, passando para o outro lado da igualdade multiplicando, então:
Aplicando a propriedade distributiva:
Resolvendo a equação de primeiro grau:
Então se ''x'' é 8, vamos testá-lo na condição de existência:
C.E:
8 + 8 > 0
e
8 - 6 > 0
Inequações verdadeiras, portanto a solução da equação é: S={8}
Verifique na equação para se certificar se está correto, substitua ''x'' por 8 e veja:
8+8 = 16 e 8-6 = 2, então temos:
Log de 16 na base 2 é 4 e log de 2 na base 2 é 1, então:
Equação verdadeira.
E temos também os casos que devemos aplicar a quarta propriedade logarítmica, e isso quando temos uma igualdade entre logaritmos de bases diferentes e um número real (ou uma incógnita), por exemplo:
Você viu que há como resolver as equações de duas maneiras diferentes: Aplicando a definição, ou simplesmente ignorando as bases (que devem ser iguais) mas e o que fazer em casos como este, em que temos bases diferentes?
Primeiramente vamos aplicar a quarta propriedade dos logaritmos: A propriedade da mudança de base.
Veja que neste caso temos duas bases diferentes nesses logaritmos: Base 3 e base x.
Vamos mudar a base deste logaritmo que contia uma incógnita em sua base, no caso, log de 9 na base x.
Aqui, a melhor base a ser escolhida é a base 3, que aparece em outro logaritmo nessa mesma equação, então aplicando a propriedade teremos:
Agora vamos resolver log de 9 na base 3:
A equação fica assim:
Neste momento nós podemos utilizar o artificio da equação (visto na aula anterior sobre logaritmos) para substituir log de x na base 3 (que aparece duas vezes na equação) por uma variável qualquer, por exemplo ''y'':
Então dizemos que:
Nossa equação fica assim:
Eliminando o denominador da fração, teremos:
Nesta equação do 2o grau, podemos aplicar Bháskara:
Então encontramos duas soluções para ''y'': -1 e 2.
Vamos verificar se ambas poderão satisfazer a equação?
Lembrando nosso artifício:
Vamos verificar primeiramente ''2'' para ''y'':
Segundo a C.E para o logaritmando:
x > 0
Se ''9'' é ''x'', então:
9 > 0
E devemos aplicar a C.E para a base também pois, temos uma incógnita na base também. A C.E para a base é:
x > 0
x ≠ 1
Então:
9 > 0 e 9 ≠ 1
Tudo certo! Então ''9'' é uma das soluções para a equação.
Iremos verificar agora ''-1'':
C.E do logaritmando:
1/3 > 0
Certo, porque 1/3 = aproximadamente à 0.34 (que é maior que zero, sim)
E para a base:
1/3 > 0 e 1/3 ≠ 1
Então ''-1'' também é a raiz da equação, fazendo com que o conjunto solução seja: S={1/3; 9}
Se quiser verificar a verdade da equação, substitua ''x'' por 9 ou 1/3 nas equações e verifique por si só:
Substituindo 9 por ''x'':
Log de 9 na base 3 é dois (como visto neste mesmo exercício) e log de 9 na base 9 é 1, então:
Equação verdadeira!
E agora, substituindo ''x'' por 1/3:
Vamos calcular log de 1/3 na base 3:
E encontrar log de 9 na base 1/3:
Então a equação fica assim:
-1 = 1 + (-2)
-1 = 1 - 2
-1 = -1
Equação verdadeira também! Portanto, as raízes estão corretas.




0 comentários:
Postar um comentário